在进行深层神经网络的计算过程中,现在主流框架(比如TensorFlow、Pytorch、MXNet等)提供了自动求导函数,极大地简化了深度学习模型训练算法的实现。但求导,又称反向传播(back-propagation),是Deep Learning中的一个重要概念,所以在这一篇文章中主要用数学和计算图两个方式来描述正向传播和反向传播。我们将使用一个带有L2范数正则化的单隐藏层感知机为例解释正向传播和反向传播。
网络结构图如下
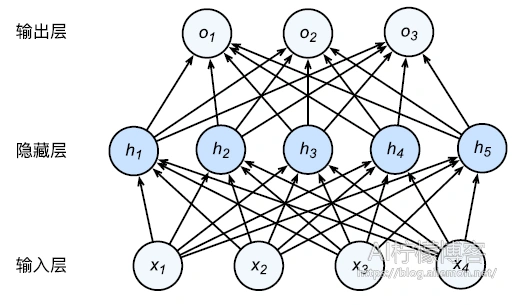
正向传播
正向传播指的就是对神经网络沿着从输入层到输出层的顺序,依次计算并存储模型中间变量。比如我们假设输入的一个特征X是d维的样本。(为了简化,我们先忽略隐藏层中的偏置bias)我们先计算中间变量
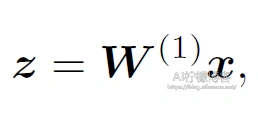 Ø其中是h x d维度的模型参数。
Ø其中是h x d维度的模型参数。
然后我们将中间变量Z应用按元素操作的激活函数Ø后,得到向量长度为h的隐藏层变量![]()
可以看出隐藏层变量H也是中间变量,且是h维的。最后通过输出层参数模型W2可以得到向量长度为q的输出层变量
![]()
接下来我们定义损失函数为L = ℓ(o; y):其中y是样本标签。根据L2番薯正则化的定义,给超参数 λ ,正则化项即
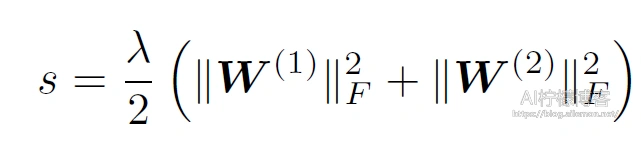
最终,模型在给定的数据样本上带正则化的损失为J = L + s
反向传播
反向传播的过程中,根据微分中的链式法则,沿着从输入层到输出层的顺序,依次计算并存储目标函数有关神经网络各层中的变量以及参数的梯度
对于输入输出X,Y,Z为任意形状张量的函数Y = f(X) 和 Z = g(Y),通过链式法则,我们可以看出
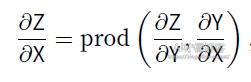
回顾一下本节中的样例模型,它的参数是W1和W2,因此反向传播的⽬标是计算ðJ/ðW1,ðJ/ðW2。
首先,分别计算目标函J = L + s有关损失项L和正则项s的梯度
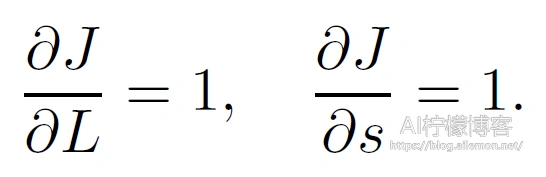
其次,依据链式法则计算⽬标函数有关输出层变量的梯度ðJ/ðo
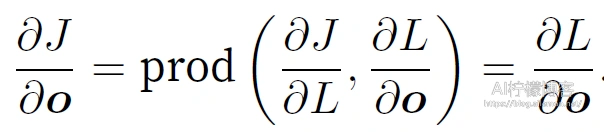
接下来,计算正则项有关两个参数的梯度:
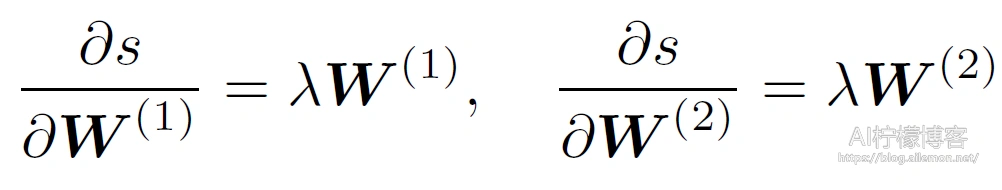
现在,我们可以计算最靠近输出层的模型参数的梯度
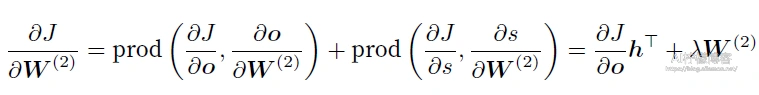
沿着输出层向隐藏层继续反向传播,隐藏层变量的梯度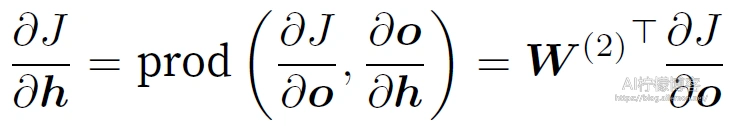
由于激活函数ϕ 是按元素操作的,中间变量z 的梯度ðJ/ðz的计算需要使⽤按元素乘法符
![]()
最终,我们可以得到最靠近输⼊层的模型参数的梯度ðJ/ðW1
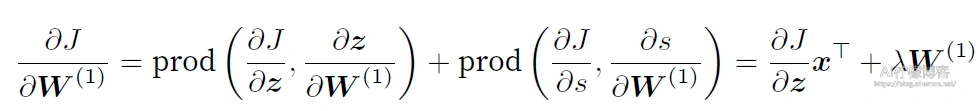
⼩结
- 正向传播沿着从输⼊层到输出层的顺序,依次计算并存储神经⽹络的中间变量。
- 反向传播沿着从输出层到输⼊层的顺序,依次计算并存储神经⽹络中间变量和参数的梯度。
参考文献
Gluon 动手深度学习 —–李沐
| 版权声明本博客的文章除特别说明外均为原创,本人版权所有。欢迎转载,转载请注明作者及来源链接,谢谢。本文地址: https://blog.ailemon.net/2018/10/22/neural-network-backward-propagation/ All articles are under Attribution-NonCommercial-ShareAlike 4.0 |

