语音声学特征提取：MFCC和LogFBank算法的原理

几乎任何做自动语音识别的系统，第一步就是对语音信号，进行特征的提取。通过提取语音信号的相关特征，有利于识别相关的语音信息，并丢弃携带的其他不相关的所有信息，如背景噪声、情绪等。

       我们都知道，人类说话是通过体内的发声器产生的初始声音，被包括舌头和牙齿在内的其他物体形成的声道的形状进行滤波，从而产生出各种各样的语音的。传统的语音特征提取算法正是基于这一点，通过一些数字信号处理算法，能够更准确地包含相关的特征，从而有助于后续的语音识别过程。常见的语音特征提取算法有MFCC、FBank、LogFBank等。

1 MFCC

       MFCC的中文全称是“梅尔频率倒谱系数”，这种语音特征提取算法是这几十年来，最常用的算法之一。这种算法是通过在声音频率中，对非线性梅尔刻度的对数能量频谱，进行线性变换得到的[1]。

MFCC特征提取算法的主体流程如下：

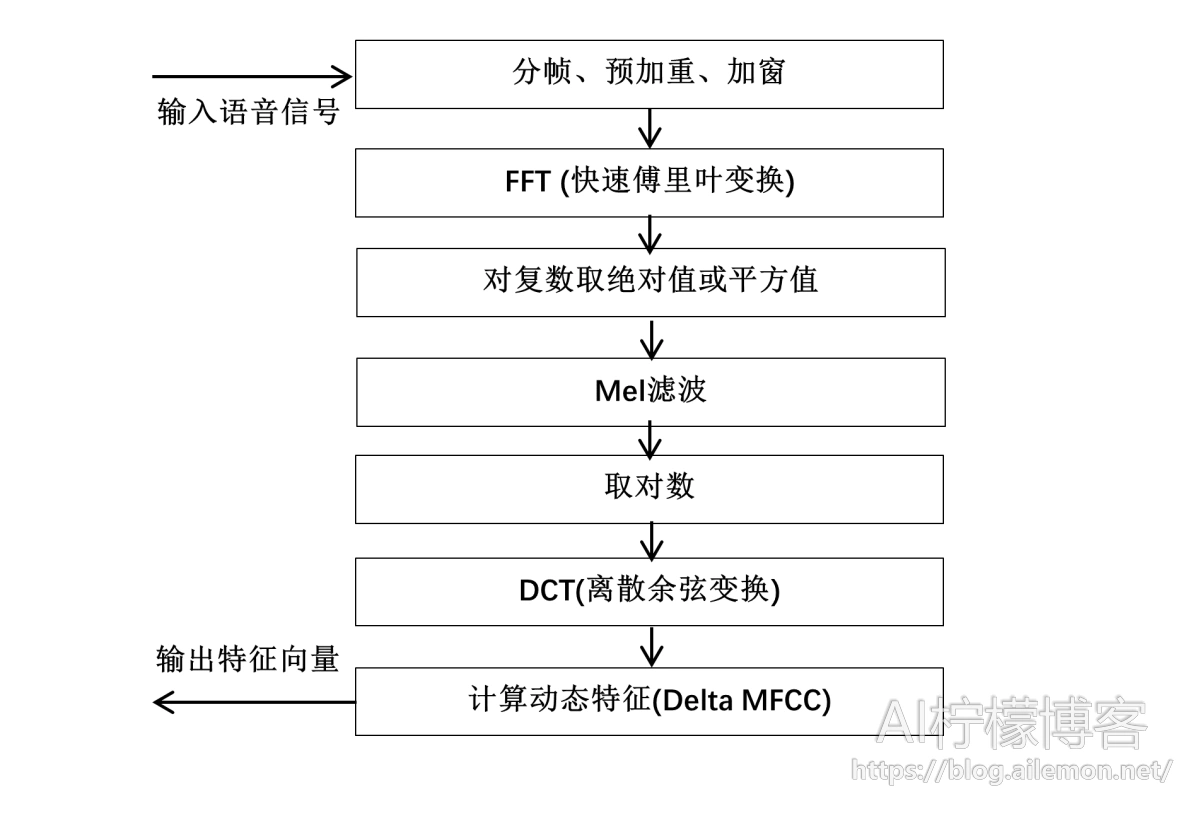
1.1 分帧

       由于存储在计算机硬盘中的原始wav音频文件是不定长的，我们首先需要将其按一定方法切分为固定长度的多个小片段，也就是分帧。根据语音信号变化迅速的特性，每一帧的时间长度一般取10-30毫秒，以保证一帧内有足够多的周期，且变化不会过于剧烈，因此，更适合这种适用于分析平稳信号的傅里叶变换。由于数字音频的采样率不同，分帧所得的每一帧向量的维度也不同。

       为了避免时间窗的边界导致信息遗漏的问题，因此，在对从信号中取每一帧的时间窗进行偏移的时候，帧和帧之间需要有一部分的重叠区域。这个时间窗的偏移量，我们一般取为帧长的一半，即每一步都偏移一帧的大约二分之一之后的位置，作为时间窗取下一帧的最终位置。这样做的好处是，避免了帧与帧之间的特性变化过大。

       通常来说，我们选取时间窗长度为25毫秒，时间窗的偏移量为10毫秒。

1.2 预加重

       由于声音信号从人的声门发出后，存在12dB/倍频程的衰减，在通过口唇辐射后，还存在6dB/倍频程的衰减，因而在进行快速傅里叶变换之后，高频信号部分中的成分较少。所以，对语音信号进行预加重操作，其主要目的是加强语音信号的每一帧中，那些高频部分的信号，以提高其高频信号的分辨率。我们需要通过采用如下公式的一阶高通滤波器进行预加重操作：
\( H(z)=1-\alpha \times z^{-1} \tag{1}\)
\( S(n)=S(n)-\alpha \times S(n-1) \forall n \in N \tag{2}\)

在上式中，\(\alpha\)是预加重的系数，其一般的取值范围是0.9 < \(\alpha\) < 1.0，通常取0.97。n表示当前处理的是第n帧，其中，第一个n=0的帧需要特别处理。

1.3 加窗

       在之前的分帧过程中，直接将一个连续的语音信号切分为若干个片段，会造成截断效应产生的频谱泄漏，加窗操作的目的是消除每个帧的短时信号在其两端边缘处出现的信号不连续性问题。MFCC算法中，选取的窗函数通常是汉明窗，也可以使用矩形窗和汉宁窗。需要注意的是，预加重必须在加窗之前进行。

汉明窗的窗函数为：
\( W(n)=0.53836-0.46164 \times \cos(\frac{2 \pi n}{N-1}) (0 \le n \le N, n=0,1,2,\dots,N) \tag{3}\)
加窗过程为：
\( S^{\prime}(n)=W(n) \times S(n) \tag{4}\)

1.4 快速傅里叶变换

       在经过上述的一系列的处理过程之后，我们得到的仍然是时域的信号，而时域中可直接获取的语音信息量较少。在进行进一步的语音信号特征提取时，还需要将每一帧的时域信号对应转换到其频域信号。对于存储在计算机上的语音信号，我们需要使用离散的傅里叶变换，由于普通的离散傅里叶变换的计算复杂度较高，通常使用快速傅里叶变换来实现。由于MFCC算法经过分帧之后，每一帧都是短时间内的时域信号，所以这一步也成为短时快速傅里叶变换。
\( P(n)=\sum_{k=0}^{N-1}{S(n) \times e^{-j \cdot \frac{2\pi kn}{N}} } (0 < n < N) \tag{5}\)

       根据奈奎斯特定理，如果要再次从离散的数字信号无损地转换到模拟信号上，在对模拟信号进行采样时，我们需要采用模拟信号最高频率值的2倍以上的采样率，对模拟信号进行模数转换的采样。对于语音识别常用的16kHz采样率音频，傅里叶变换之后的频率范围为0到8kHz之间。

1.5 计算幅度谱(对复数取模)

       在完成了快速傅里叶变换之后，得到的语音特征是一个复数矩阵，它是一个能量谱，由于能量谱中的相位谱包含的信息量极少，所以我们一般选择丢弃相位谱，而保留幅度谱。

       丢弃相位谱保留幅度谱的方法一般是两种，对每一个复数求绝对值或者求平方值。
\( P^{\prime}(n)=\sqrt{P^2_{(n)}} \tag{6}\)
\( P^{\prime}(n)=P^2_{(n)} \tag{7}\)

1.6 Mel滤波

       Mel滤波的过程是MFCC和fBank特征的关键之一。Mel滤波器是由20个三角形带通滤波器组成的，将线性频率转换为非线性分布的Mel频率。

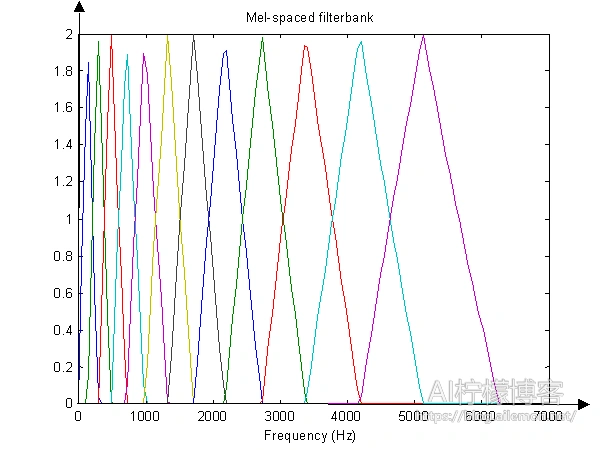
Mel倒谱公式：
\( Mel(f)=2595 \times \log_{10} (1+\frac{f}{700}) = 1125 \times \ln (1+\frac{f}{700}) \tag{8}\)
梅尔滤波器：
\(
B_m[k] = \begin{cases}
0 & k < f_{m-1}或k>f_{m+1} \\
\frac{k-f_{m-1}}{f_m-f{m-1}} & f_{m-1} \le k \le f_m \\
\frac{f_{m+1}-k}{f_{m+1}-f_m} & f_m \le k \le f_{m+1}
\end{cases} \tag{9}\)

Mel滤波公式：
\( E_m=\ln ( \sum_{k=0}^{N-1} {P(k) \times H_m(k)} ) \tag{10}\)

经过Mel滤波之后，Em即为得到的fBank特征。

   1.7 取对数

       在得到上一步的fBank特征之后，由于人耳对声音的感受是成对数值增长的，所以需要将数值再进行一次对数运算，以模拟人耳的感受。我们需要对纵轴通过取对数进行缩放，可以放大低能量处的能量差异。

   1.8 离散余弦变换

       离散余弦变换是MFCC相对于fBank所特有的一步特征提取运算。在上一步取了对数之后，我们还需要对得到的N维特征向量值，再进行一次离散余弦变换(DCT)。做DCT的根本原因是，不同阶数信号值之间具有一定的相关性，而我们需要去掉这种相关性，将信号再映射到低维的空间中。由于最有效的特征聚集在前12个特征里，所以在实际中，一般仅保留前12-20个结果值，通常取13个，这样一来，就进一步压缩了数据。 离散余弦变换公式如下：
\( C_i=\sqrt{ \frac{2}{N} } \sum_{j=1}^{N} E_j \times \cos ( \frac{\pi \cdot i}{N} \cdot (j-0.5) ), \forall i \in [1,M] \tag{11}\)

1.9 计算动态特征

       上述MFCC算法仅仅体现了MFCC的静态特征，而其动态特征还需要使用静态特征的差分来表示。通过将得到的动态的特征，和前一步得到的静态特征相结合，可以有效地提高这种语音识别系统的识别性能。 差分参数的计算公式：
\( d_t= \begin{cases}
C_{t+1}-C_t & t<K \\
\frac{ \sum_{k=1}^{K} k(C_{t+k}-C_{t-k}) }{ \sqrt{2 \sum_{k=1}^K k^2} } & other \\
C_t-C_{t-1} & t \ge Q-K
\end{cases} \tag{12}\)

式中,\(d_t\)是第t个一阶差分值，\(C_t\)是第t个倒谱系数值，Q是倒谱系数的最大阶数，K是一阶差分的时间差，一般可取1或取2。二阶差分则将上式的结果再代入进行计算即可。

       最后，再将静态特征和动态特征的一阶、二阶差分值合并起来，当静态特征是13维的特征向量时，合并动态特征后，总共有39维特征。

2 logfBank

       logfBank特征提取算法类似于MFCC算法，都是基于fBank特征提取结果的基础上，再进行一些处理的。不过logfBank跟MFCC算法的主要区别在于，是否再进行离散余弦变换。logfBank特征提取算法在跟上述步骤一样得到fBank特征之后，直接做对数变换作为最终的结果，计算量相对MFCC较小，且特征的相关性较高，所以传统的语音识别技术常常使用MFCC算法。

       随着DNN和CNN的出现，尤其是深度学习的发展，由于fBank以及logfBank特征之间的相关性可以更好地被神经网络利用，以提高最终语音识别的准确率，降低WER，因此，可以省略掉离散余弦变换这一步骤。

3 总结

本文主要介绍了MFCC和LogFBank语音特征提取算法的数学原理及计算过程方法，之后AI柠檬博客还将更新另一种语音识别特征提取算法：语谱图特征，敬请期待！

参考资料 Refference

1. Davis S, Mermelstein P. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences[J]. IEEE transactions on acoustics, speech, and signal processing, 1980, 28(4): 357-366.

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2021/03/01/speech-acoustic-feature-extraction-the-principle-of-mfcc-and-logfbank-algorithm/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate