看懂语音识别中CTC解码器的原理，这篇文章就够了

在DNN-HMM架构的语音识别系统的声学模型中，训练一个DNN模型通常需要先进行帧和标签的对齐操作，此时需要先使用GMM通过EM算法不断迭代实现。而且隐马尔可夫假设一直饱受诟病，随着深度学习的发展，尤其是基于CTC的CNN和RNN模型的出现，使得实现端到端的语音识别声学模型成为了可能。CTC由于其强大的在时间序列上进行标签自动对齐的能力，可被用于语音识别、图像验证码(或者文本)识别和视频手势识别(手语识别)等问题中。

1 CTC的基本原理

CTC是英文Connectionist Temporal Classification的首字母缩写，中文翻译为“连接时序分类”。通过CTC，可以直接将语音在时间上的帧序列和相应的转录文字序列在模型训练过程中自动对齐，无需对每个字符或音素出现的起止时间段做标注，以实现直接在时间序列上进行分类，也免去了传统算法较为复杂的对齐操作。

CTC方法主要分为两个部分，一个是训练时的标签对齐和损失函数loss值的计算，一个是推理解码时计算得到最终的预测结果。其中，解码部分分为三种，贪婪法(Greedy)、束搜索法(Beam Search)和前缀束搜索法(Prefix Beam Search)。其中，最常用的则是简单高效的贪婪法。通过在每个时间步上寻找概率最大的值作为最终预测的输出并去掉连续重复和空白块即可。而基于CTC loss的训练算法由于实现较为复杂，一般都直接使用已有的计算框架来做。

AI柠檬博主曾翻译过一篇详细讲解CTC内部底层原理的论文，推荐大家看一看：https://blog.ailemon.net/2019/07/18/sequence-modeling-with-ctc/

2 CTC数学原理

CTC的每个单一对齐的时间步上的概率公式为：

\( p(\pi|x)=\sum^T_{t=1}{y^{t}_{\pi_t}}, \forall \pi \in L’^{T} \tag{1} \)

其中，π为冗余的文本字符序列或者音素序列，在中文语音识别中还可以为拼音序列，x则表示语音的输入，y表示神经网络部分的输出。因为连续的很多帧都可以对应同一个字，或者输出为空，因此通过定义一个多对一的函数，将神经网络输出序列中重复的字符进行合并，得到一个唯一的输出序列。对于一个(X,Y)的元组，CTC目标函数公示表示为：

\( p(l|x)=\sum_{\pi \in R^{-1}(l)} p(\pi|x) \tag{2} \)

其中，Y为对应的标注文本。我们的目标是在输入x的前提下，从l处开始到最后一个T处，最大化p(y|x)函数值的参数。这可以通过使用前向后向算法来解决。

我们需要基于最大概率路径来纠正最大概率的标签：

\( h(x) \approx B(\pi^*) \tag{3} \)

当 \( \pi^{∗} = \mathop { \arg \max} \limits _{\pi \in N^t} p(\pi|x) \)时 .

其中，前向因子为：

\( \alpha_t (s) \stackrel{\rm def}{=} \sum \limits_{\pi \in N^T : B(\pi_{1:t})=l_{1:s}}{ \prod \limits_{t’ =1} \limits^{t} { y^{t’}_{\pi_{t’}} } } \tag{4} \)

后向因子为：

\( \beta_t(s) \stackrel{\rm def}{=} \sum \limits_{\pi \in N^T : B(\pi_{t:T})=l_{s:|l|}}{ \prod \limits_{t’ =t} \limits^{T} { y^{t’}_{\pi_{t’}} } } \tag{5} \)

有

\( \alpha_t (s) \beta_t(s) = \sum \limits_{\pi \in B^{-1}(l) : T_t=l’_s}{ y_{l’_s}^t \prod \limits_{t’ =1} \limits^{T} { y^{t}_{\pi_{t}} } } \tag{6} \)

那么CTC的输入输出和前后向因子的关系为：

\( p(l|x)= \sum \limits^{|l’|} \limits_{s=1} {\frac{ \alpha_t (s) \beta_t(s) }{y^t _{l’_s}}} \tag{7} \)

对其进行求偏导有

\( \frac{\partial p(l|x)}{\partial y^{t}_{k}} = \frac{1}{y^{t^2}_k} \sum \limits_{s\in lab(1,k)} {\alpha_t(s)\beta_t(s)} . \tag{8} \)

从而可以对参数使用梯度下降算法进行梯度更新。

3 CTC解码算法

在声学模型通过计算得到输出结果之后，通常需要使用CTC解码器进行解码，主流深度学习框架都内置有CTC的解码器，一般都为贪婪搜索和束搜索解码。

3.1 贪婪搜索(Greedy Search)

贪婪搜索为CTC解码算法中，最简单的一种解码方式。贪婪算法本质上就是每一步都要最好的，也就是解码时直接取每一个时间步中，输出概率最大的那一个符号，作为最终的结果。

由于在实际计算过程中，直接计算得一条最佳的输出较为复杂，但是对于一个具体的字符Π，神经网络都会在每一个时间步上输出其预测的概率值，因此，简化的算法直接认为概率最大的项即为正确的预测。算法的时间复杂度为O(t*N)，其中t为时间步的长度，N为字符类别数。

表1 一个CTC输入样例

	0	1	2	3	4	5	6	7	8
a	0.990	0.020	0.012	0.005	0.001	0.031	0.001	0.001	0.000
b	0.001	0.001	0.001	0.001	0.000	0.000	0.000	0.000	0.000
c	0.001	0.060	0.980	0.991	0.023	0.000	0.000	0.000	0.000
d	0.001	0.001	0.001	0.001	0.000	0.000	0.000	0.000	0.000
e	0.001	0.001	0.001	0.001	0.000	0.000	0.000	0.000	0.000
f	0.005	0.002	0.000	0.000	0.000	0.926	0.997	0.947	0.002
g	0.001	0.004	0.004	0.001	0.002	0.001	0.000	0.021	0.001
_	0.000	0.910	0.001	0.000	0.974	0.042	0.002	0.031	0.997

其中，横向为时间步，纵向为每一个时间步中，所有可能字符的概率向量。

根据贪婪搜索算法，在每一个时间步上取概率最大的项，样例中，可以得到这样的一个序列：

a_cc_fff_

最后，去掉连续重复的字符，以及空白分隔符号，即可得到CTC解码后，最终的预测结果：“acf”。

3.2 束搜索(Beam Search)

贪婪算法的最大问题就是简单粗暴地取每一个时间步中概率最大的元素作为输出，而且只能得到一条由所有最大概率字符组成的结果。没有起到充分利用上下文信息的作用，不能够根据上下文选择最合适的输出字符，在语音识别实际应用中常常会出现选择了一个读音相近的字音，而不是这里本应该出现的正确字音。

而改进的CTC解码使用束搜索算法，在最终解码的结果中，通过将所有字符出现的排列组合时，对概率进行累积，得到一个最终的概率，并按概率值的大小进行排序，以提供多种选择给用户。不过由于束的大小会随着排列组合时，时间步的数量成指数型增长，一般会对搜索束限定一个最大的宽度，常常取为100个，即每次计算仅保留概率最大的前100条临时结果。算法的时间复杂度为O(t*m*N)，其中t为时间步的长度，m为搜索束的最大宽度，N为字符类别数。

我们还是以上述样例为例，选取最大的束宽度为2，搜索过程为：

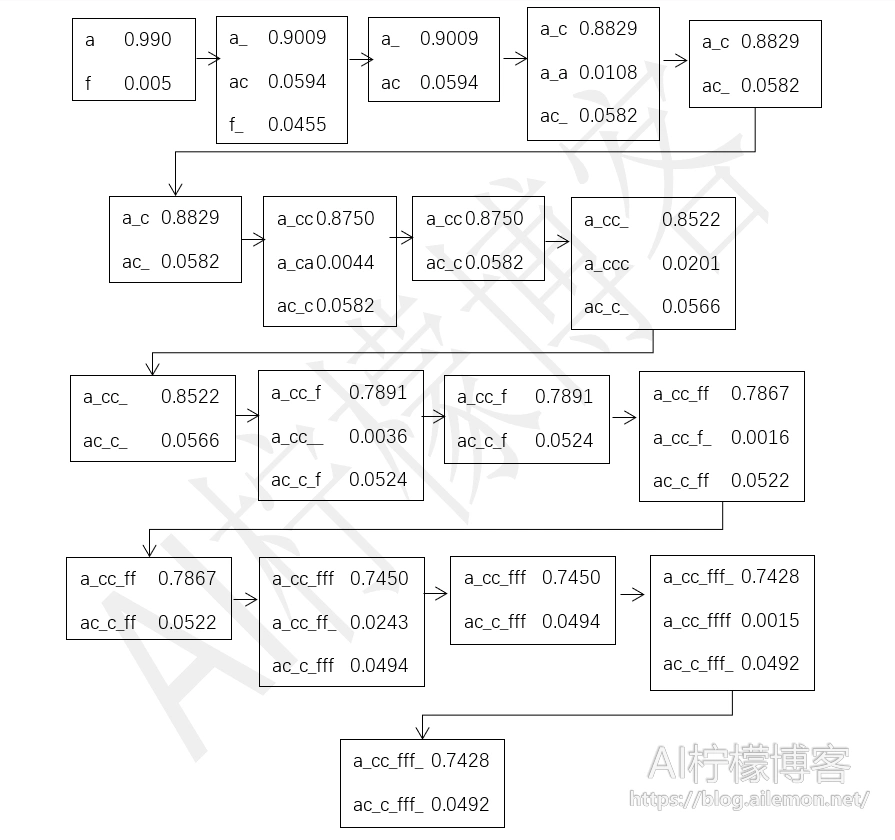
最终得到概率最大的两条序列，分别为“acf”和“accf”。其中，第一条序列跟直接用贪婪搜索算法得到的结果一模一样，因为都是用概率最大的值计算得到的。而第二条则是一个备选结果，其概率仅次于最佳结果。有了多个备选结果之后，就可以通过外接语言模型来做进一步的计算，以得到最佳的输出结果。

3.3 前缀束搜索(Prefix Beam Search)

对于普通的束搜索存在一个明显的问题，例如在进行束搜索算法过程中，对于可能的两个中间结果“_ac”和“aac”，他们在解码之后有着相同的前缀“ac”，对于中间结果的计算时，他们其实应该合并为同一条，否则会减少搜索结果的多样性，甚至会导致由于两个相同前缀的结果分摊了概率值，影响声学模型最终的识别率。在这种情况下，我们通过在搜索过程中不断合并中间结果中出现相同前缀的结果，并将他们的概率加和。算法的时间复杂度为O(t*m*N)，其中t为时间步的长度，m为搜索束的最大宽度，N为字符类别数。

通过将搜索前缀合并，使得算法的搜索束更加多样化，最终也会返回若干个最佳解码结果，然后再通过外接语言模型进一步计算，选取一个最佳的输出结果。

4 总结

正如刚才提到的那篇论文原文中写的，CTC最常被提及的缺点之一是它所做的条件独立性假设。该模型假设每个输出在条件上独立于给定输入的其他输出。 对于许多seq2seq问题，这是一个不好的假设。

另外，CTC算法是无对齐的，目标函数在所有对齐上边缘化。虽然CTC确实对X和Y之间的对齐形式做出了强有力的假设，但该模型对于如何在它们之间分配概率是不可知的。CTC对齐的另一个重要特性是它们是多对一的。多个输入甚至可以对齐到一个输出。在某些情况下，这可能并不可取。我们可能希望在X和Y的元素之间强制执行严格的一对一对应关系。或者，我们可能希望允许多个输出元素与单个输入元素对齐。例如，字符“th”可能与音频的单个输入步骤对齐。基于字符的CTC模型不允许这样做，而应该使用基于“编码器——解码器”的模型。

乍一看，隐马尔可夫模型（HMM）似乎与CTC完全不同。但是，这两种算法实际上非常相似。了解它们之间的关系将有助于我们了解CTC对HMM序列模型的优势，并让我们深入了解如何针对各种用例更改CTC。

最后，即使对CTC有充分的了解，实现也是很困难的，所以往往都是直接调库。朴素地计算CTC损失在数值上是不稳定的，避免这种情况的一种方法是在每个时间步正则化α。使用beam搜索解码器时的常见问题是要使用的beam的大小，需要在准确性和运行时间之间存在权衡。由于Beam搜索的特性，在实现和使用CTC的beam搜索时，需要掌握一些好的技巧，详细可看上述文章“从业者指南”中相关内容。

参考文献

1. Hannun A. Sequence modeling with ctc[J]. Distill, 2017, 2(11): e8.
2. Graves A, Fernández S, Gomez F, et al. Connectionist temporal classification: labelling unsegmented sequence data with recurrent neural networks[C]//Proceedings of the 23rd international conference on Machine learning. ACM, 2006: 369-376.

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2020/10/26/asr-ctc-decoder-theory/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate