卷积神经网络相关计算总结，都在这了

卷积神经网络是模式识别分类常用的网络结构之一，在大规模的图像识别等方面有着很大的优势。本文将总结卷积层、反卷积层、感受野、权重参数数量等卷积神经网络相关的原理和计算过程。

卷积层

valid卷积

valid卷积是最常用的下采样卷积，其特点是卷积核不能超出特征图的范围。如图，在卷积核为3×3且步长为1，且不会在周边增加扩充值的情况下，一个5×5的特征图经过卷积后，变成了3×3的尺寸大小。

其计算过程如下：

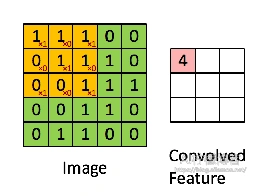
输出的特征图维度 \( D_{output} \) 计算式为：

–\(D_{output} = \frac{D_{input} – D_{kernel} + 2 Padding}{S_{kernel}} +1    \tag{1}\)–

其中， \( S_{kernel} \) 代表卷积核的步长， \( D_{kernel} \) 代表卷积核的维度， \( Padding \) 代表扩充值的维度。

full卷积

full卷积式典型的上采样卷积，其特点式卷积核可以超出特征图的范围，但是卷积核的边缘要与特征图的边缘有交点。这种卷积将如图的2×2的特征图，在经过尺寸为3×3、步长为1的卷积核卷积后，变成了4×4的特征图。其输出特征维度的计算仍然满足式(1)。

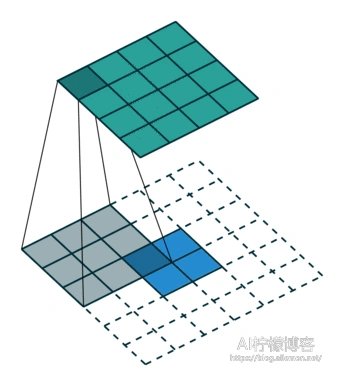
same卷积

same卷积是介于full卷积和valid卷积之间的一种卷积方式，其特点是卷积前后特征图的尺寸不变。由于same卷积的特点，其Padding值是固定设置的，计算式可通过式(1)推导出来。

–\(Padding = \frac{1}{2} ( \frac{n-1}{S_{kernel}} – n + D_{kernel} )    \tag{2}\)–

其中，n是输入或输出特征图的尺寸。

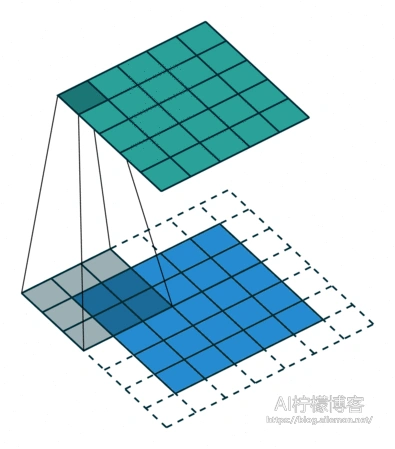
我们可以下面这个例子表述其卷积计算方式：

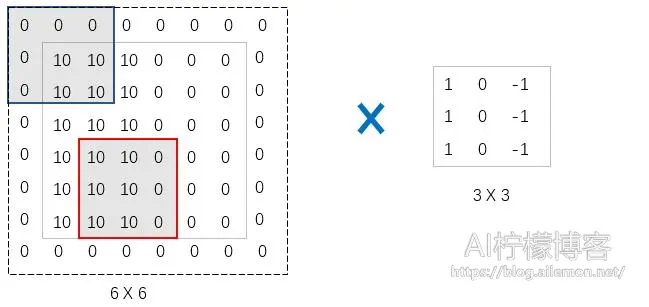
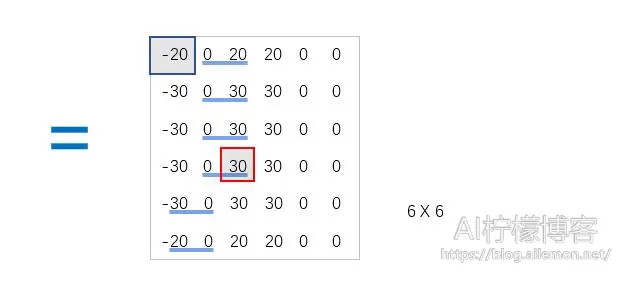
反卷积层

反卷积是一种常用的上采样方法。反卷积可以将图像恢复到卷积之前的尺寸，输出尺寸的计算式为：

–\( D_{output} = S_{kernel} × (D_{input} – 1) + D_{kernel} – 2 × Padding + offset    \tag{3}\)–

其中，

–\( offset = (D_{output} – 2 × Padding – D_{kernel}) \% S_{kernel}    \tag{4} \)–

并且\(S_{kernel} ≠1\).

在反卷积的计算中，其操作会先对输入进行填充，再进行正常的卷积操作。假设我们有这样的一个输入特征图

1	1	1
1	1	1
1	1	1

和3×3的卷积核

1	1	1
1	1	1
1	1	1

如果我们设定\(S_{kernel} = 1 \) ，Padding = “SAME”，那么，在其输入特征图每个点周围不需要填充0，只需在周边补0，例如：

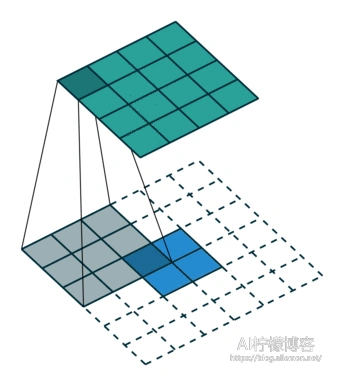
看起来跟上采样的full卷积差不多，但实际意义不同。当 \( S_{kernel} = 2 \) ，Padding=”SAME”时，首先时在每个输入的元素之间填充0，个数为： \( S_{kernel} – 1 \) ，填充结果如下。

1	0	1	0	1
0	0	0	0	0
1	0	1	0	1
0	0	0	0	0
1	0	1	0	1

如果设置输出的尺寸为5×5，那么使计算的输出尺寸与设置的输出尺寸相同，那么输出为：

1	2	1	2	1
2	4	2	4	2
1	2	1	2	1
2	4	2	4	2
1	2	1	2	1

计算演示过程如下

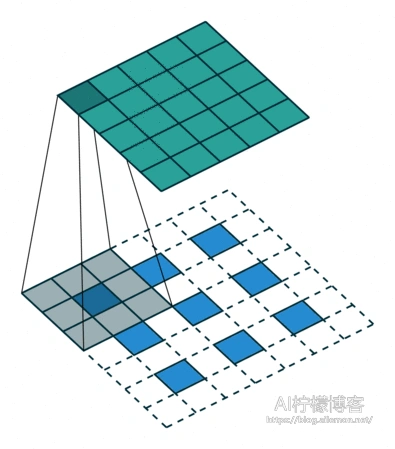
如果输出尺寸为6×6，使计算的输出尺寸比设置的输出尺寸小且宽和高各相差1，那么还需要对输入的右列和下行填充0，如图。

池化层

池化通常有：最大池化、平均池化、重叠池化、空间金字塔池化。

最大池化顾名思义就是，每次从中取最大值作为输出结果。以滤波器大小为2×2以及步长为2为例，如下图所示。

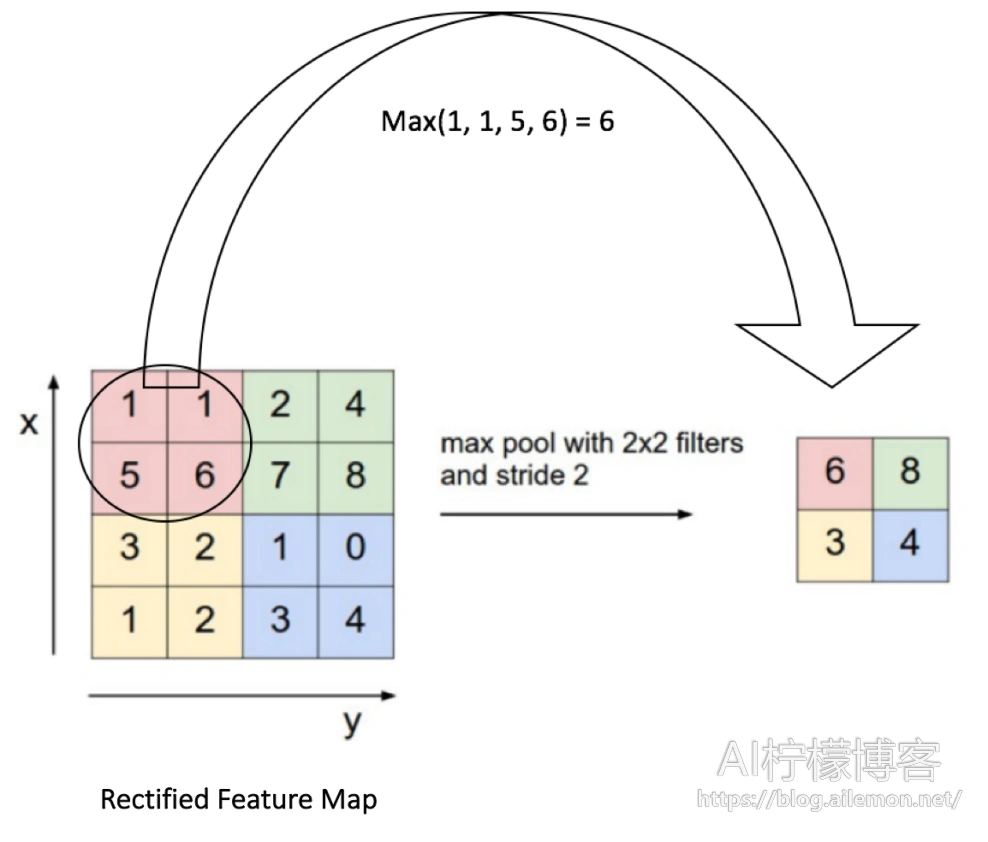
平均池化是将几个数计算平均数后作为输出结果，如图。

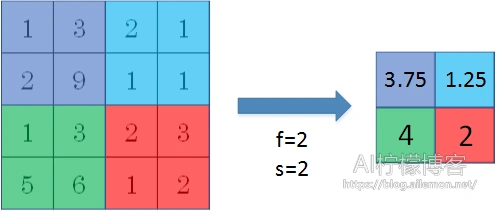
而重叠池化，则是上述两种池化时，池化尺寸大于步长的情况，滤波器的移动有重叠，故得名。当上述两种池化步长为1时，输出尺寸为3×3而不是2×2。

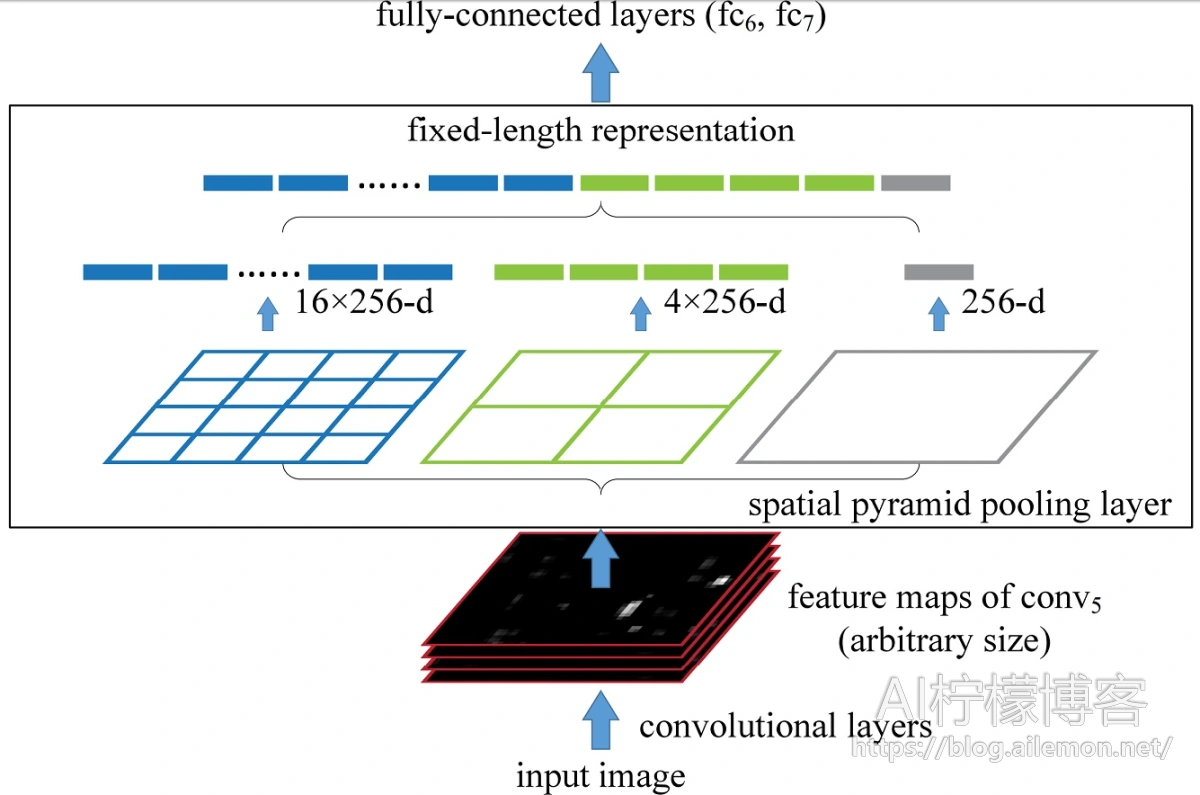
空间金字塔池化可以把任何尺度的图像的卷积特征转化成相同维度，这不仅可以让CNN处理任意尺度的图像，还能避免cropping和warping操作，导致一些信息的丢失，具有非常重要的意义。

一般的CNN都需要输入图像的大小是固定的，这是因为全连接层的输入需要固定输入维度，但在卷积操作是没有对图像尺度有限制，所有作者提出了空间金字塔池化，先让图像进行卷积操作，然后转化成维度相同的特征输入到全连接层，这个可以把CNN扩展到任意大小的图像。

感受野

感受野是某一层输出结果中，一个元素(点)所对应的输入层的区域。感受野的计算式为：

–\( r_{out} = r_{in} + (k-1)×j_{in}    \tag{5}\)–

其中， \( r_{in} \)表示输入特征图的感受野大小，k表示卷积核的大小， \(j_{in} \)表示两个连续的特征之间的距离，有

–\( j_{out} = j_{in} × stride    \tag{6}\)–

可以看到感受野的计算是一个递推的关系。

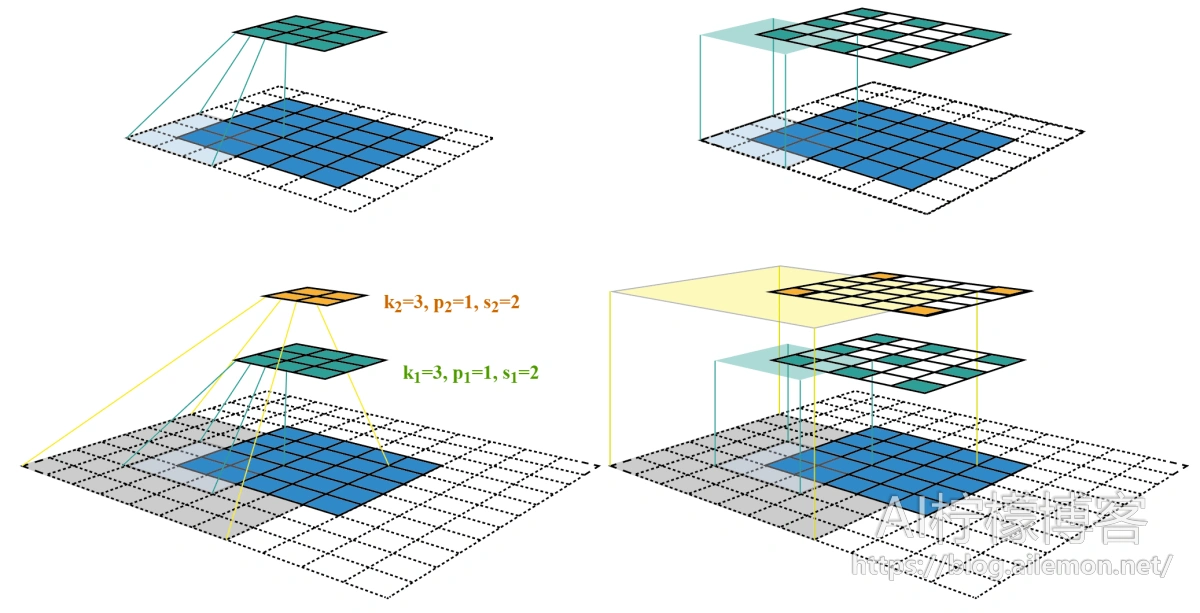
以该图为例，各层的kernel size、padding、stride超参数已在图中标出，右侧图为feature map和感受野中心对齐后的结果。第二层对应的第一层上的感受野大小为 \( r_{out} = 1 + (3-1)×1=3 \)，同样，第三层对应第一层上的感受野大小为 \( r_{out}=3+(3-1)×2=7 \) 。

权重数量计算

卷积层权重数量的计算与该层的卷积核尺寸、是否加偏置项bias、卷积核个数，以及输入层的特征深度有关。

–\( 权重数量=(depth_{in}×k_{h}×k_{w}+bias)×kernel    \tag{7}\)–

其中， \(depth_{in} \)是输入层特征深度， \(k_h \)是卷积核尺寸的第一维， \(k_w \)是卷积核尺寸第二维， \(bias \)为是否使用偏置项，使用时为1，否则为0， \( kernel \)为该层卷积核个数，也就是输出特征图的深度。

比如，输入层的特征图维度是(224,  224, 3)，第一层卷积的配置为：卷积核尺寸为3×3，使用bias项，卷积核个数为32，那么，该层的权重数量=3×(3×3+1)×32=960。

而卷积神经网络的总参数量只需要使用该方法计算所有卷积层权重数量，以及其他层权重数量之后加和即可得到。

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2020/10/12/cnn-calculation-summary/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate