原文：https://distill.pub/2017/ctc/

Hannun A. Sequence modeling with ctc[J]. Distill, 2017, 2(11): e8.

下面是连结时序分类(CTC)的一个可视化指导图，CTC是一种用于在语音识别，手写识别和其他序列问题中训练深度神经网络的算法。

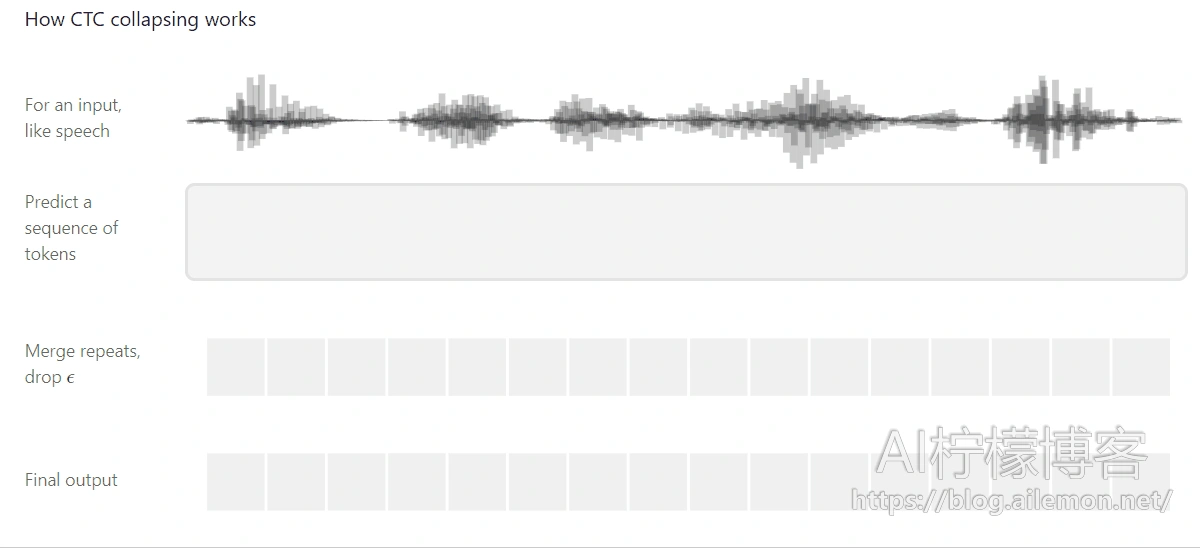
引言

对于语音识别，我们有一个声音片段和对应校正后的转写文本数据集。不幸的是，我们不知道如何将文字记录中的字符与音频对齐，这使得训练语音识别器比最开始想的看起来更难。

如果没有这种对齐, 我们就无法使用简单的方法。我们可以设计一个规则, 如 “一个字符对应于十个输入”。但人们的说话速度各不相同, 所以这种规则总是会失效的。另一种选择是将每个字符与其在音频中的位置进行手动对齐。从建模的角度来看, 这很管用——我们知道每个输入时间步长对应的真实值。但是, 对于任何规模稍大的数据集, 都会非常耗时。

这个问题不仅仅出现在语音识别中。我们在其他很多地方都能看到。从笔划的图像或序列进行手写识别就是一个例子，视频中的动作标签则是另一个例子。

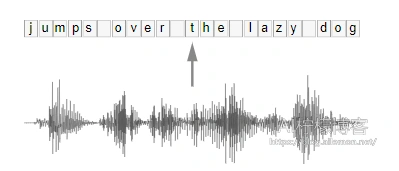
连结时序分类 (CTC) 是一种不知道输入和输出之间的对齐方式。正如我们将看到的, 它特别适用于语音和手写识别等应用程序。

为了更专业一点，让我们来看一下，映射的输入序列记为X=[x1,x2,…,xt]，例如音频；对应的输出序列记为Y=[y1,y2,…yu]，例如转写文本。我们想寻找到一个从X到Y正确的映射关系。

如果我们使用更简单的监督学习算法，会遇到一些挑战。特别是:

• X和Y的长度都是变化的
• X和Y的长度比是变化的
• 我们没有一个准确的X和Y之间每个元素的对齐关系

CTC算法可以战胜这些挑战。对于一个给定的X，它就会给我们一个所有可能的Y的输出分布。我们可以使用此分布来推断可能的输出或评估给定输出的概率。

并非所有计算损失函数和执行推理的方法都是易处理的。 我们要求CTC有效地完成这两项工作。

损失函数：对于给定的输入，我们希望训练我们的模型以最大化它对齐到正确答案的概率。 为此，我们需要有效地计算条件概率p（Y | X）。 函数p（Y | X）也应该是可微的，所以我们可以使用梯度下降。

推论：当然，在我们训练模型之后，我们想用它来推断给定X时，一个可能的Y。 这意味着解决了\(Y^{*} = \mathop{\arg\max}_{Y} p(Y | X) \tag{1} \)

在理想情况下，可以有效地找到Y*值。有了CTC，我们将会找到一个代价不太大的近似解决方案。

算法

CTC算法可以为给定X的任何Y分配概率。 计算这种可能性的关键是CTC如何考虑输入和输出之间的对齐。 我们将首先来看这些对齐，然后展示如何使用它们来计算损失函数并执行推理。

对齐

CTC算法是无对齐的——它不需要输入和输出之间的对齐。 然而，为了获得给定输入的输出概率，CTC通过对两者之间所有可能的对齐的概率进行求和来实现。我们需要了解这些对齐是什么，以便了解最终如何计算损失函数。

为了说明CTC对齐的具体形式，首先来看一种朴素的方法，我们来举个例子吧。假设输入长度为6，Y = [c，a，t]。 对齐X和Y的一种方法是为每个输入的元素指定一个输出字符并合并重复。

这种方法有两个问题。

• 通常，强制每个输入元素与某些输出对齐是没有意义的。 例如，在语音识别中，输入元素可以是没有相应输出的静音段。
• 我们无法生成连续的多个字符的输出。 比如对齐的[h，h，e，l，l，l，o]，合并重复将产生“helo”而不是“hello”。

为了解决这些问题，CTC为允许的输出集引入了一个新的标记，这个标记有时被称为空标记。 我们在这里将它称为ϵ。ϵ标记与任何内容都不对应，只会从输出中删除。

CTC允许的对齐长度与输入的长度相同。 我们允许在合并重复和删除ϵ标记后映射到Y的任何对齐：

如果Y在一行序列中有两个相同的字符，那么有效的对齐必须在它们之间有一个ϵ。 有了这个规则，我们就可以区分出“hello”的合并对齐和“helo”的合并对齐。

让我们回到输出长度为6的输出[c，a，t]。 以下是有效和无效对齐的更多示例。

CTC对齐有一些值得注意的特性。首先，X和Y之间允许的对齐是单调的。如果我们前进到下一个输入，我们可以保持相应的输出相同于下一个，或前进到下一个。 第二个特性是X与Y的对齐是多对一的。 一个或多个输入元素可以对齐到单个输出元素，但是反过来则不是。 这意味着第三个特性：Y的长度不能大于X的长度。

损失函数

CTC对齐为我们提供了一种从每个时间步的概率到输出序列概率的自然方法。

确切地说，一个（X，Y）对的CTC目标函数是：\(p(Y | X) = \sum_{A\in A_{X,Y}}{\prod^{T}_{t=1}{p_{t}({a_{t} | X}) }} \tag{2}\)

注：p(Y|X)是CTC条件概率，加和是用于边缘化有效对齐集合，累积是用于逐步计算单个对齐的概率。

使用CTC训练的模型通常使用递归神经网络（RNN）来估计每个时间步长的概率，Pt（at | X）。 RNN通常效果不错，因为它考虑了输入中的上下文，但是我们可以自由地使用任何学习算法，在给定的固定大小的输入的切片上，在输出类上产生一个分布。

如果我们不小心，计算CTC损失值可能非常大。 我们可以尝试前馈的方法，并计算每个对齐的评分，将它们全部加起来。问题是可能存在大量的对齐。[1]对于大多数问题，这会很慢。

值得庆幸的是，我们可以使用动态规划算法更快地计算损失。理解的关键是，如果两个对齐在同一步上得到相同的输出，那么我们可以合并它们。

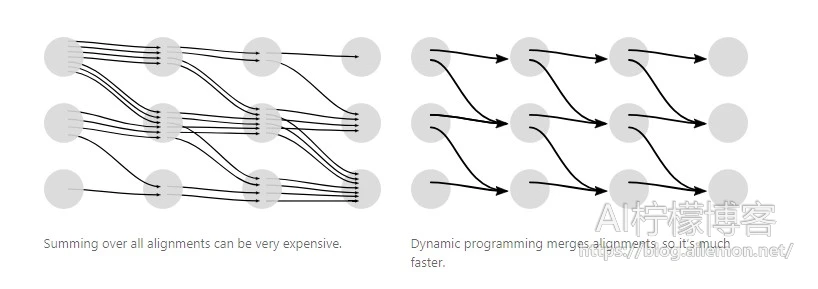
由于我们可以在Y中的任何标记之前或之后具有空白标记，因此使用包含空白标记的序列来描述算法更容易。 我们将使用序列\( Z = [\epsilon, y_1, \epsilon, y_2, \dots, \epsilon, y_U, \epsilon] \tag{3} \)

一个Y的序列，在开头，结尾和每个字符之间都有一个ϵ。

我们让α成为给定节点上合并对齐的评分。更确切地说，α{s，t}是子序列Z_ {1：s}，在t输入步骤之后的CTC得分。正如我们所看到的，我们将从最后一个时间步的α，计算最终的CTC得分P（Y | X）。 只要我们知道前一个时间步的α的值，我们就可以计算α{s，t}。这有两种情况。

情况1：

在这种情况下，我们不能跳过Z_S-1，即Z中的前驱标记。 第一个原因是，前驱标记可以是元素Y，我们不能跳过元素Y。 由于Z中Y的每个元素后跟一个ϵ，我们可以在Zs = ϵ时识别出来。第二个原因是，我们必须在Y中的重复字符之间有一个ϵ，我们可以在Zs = Z_S-2时识别出来。

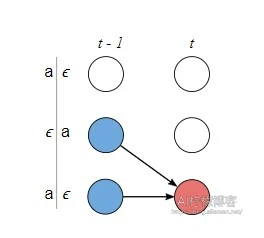
为了确保我们不跳过Z_S-1，我们既可以在前一个时间步就到那里，也可以在某个早期的时间步通过。因此，我们可以从两个位置过渡。\( {\alpha}_{s,t} = ({\alpha}_{s-1,t-1} + {\alpha}_{s,t-1}) \cdot p_t (z_s | X) \tag{4} \)

注：第一个因子是t-1输入步后两个有效子序列的CTC概率，第二个因子是输入步t当前字符的概率。

情况2：

在第二种情况下，我们允许跳过Z中的前驱标记，只要Z_S-1是不同字符之间的ϵ。 因此，我们可以在上一步中找到三个位置。

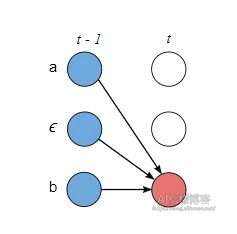
–\( {\alpha}_{s,t} = ({\alpha}_{s-2,t-1} + {\alpha}_{s-1,t-1} + {\alpha}_{s,t-1}) \cdot p_t (z_s | X) \tag{5} \)

注：第一个因子是t-1输入步后三个有效子序列的CTC概率，第二个因子是输入步t当前字符的概率。

下面是动态规划算法执行的计算示例，每个有效对齐在该图中都有一个路径。

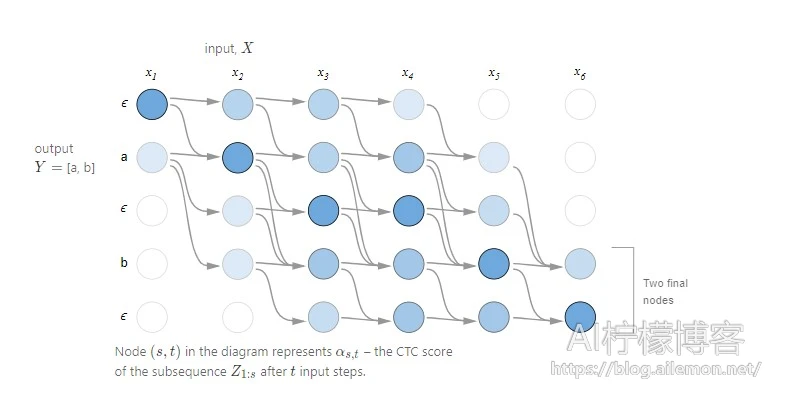
这里有两个有效的起始节点和两个有效的最终节点，因为序列开头和结尾的ϵ是可选的，全概率则是两个最终节点的总和。

现在我们可以有效地计算损失函数，下一步是计算梯度并训练模型。 CTC损失函数相对于每个时间步输出概率是可微分的，因为它只是它们的总和及乘积。鉴于此，我们可以分析计算损失函数相对于（非标准化）输出概率的梯度，并从那里开始像往常一样进行反向传播。

对于训练集D，模型的参数就转换为最小化负对数似然\( \sum_{(X, Y) \in D}{-log (p(Y | X))}  \tag{6} \)

而不是直接最大化似然。

推理

在我们训练模型之后，我们想用它来找到给定输入的可能输出。更确切地说，我们需要解决：\(Y^{*} = \mathop{\arg\max}_{Y} p(Y | X) \tag{7} \)

一种启发式方法是在每个时间步中获取最可能的输出，这给了我们最高概率的对齐：\(A^{*} = \mathop{\arg\max}_{Y} \prod_{t=1}^{T}{ p_{t}(a_t | X)}  \tag{8} \)

然后我们可以合并重复并删除ϵ标记以获得Y.

对于许多的应用，这种启发式算法效果不错，特别是当大多数概率块被分配给单个对齐时。 但是，这种方法有时会很容易错过有更大概率的输出。问题是，它没有考虑到单个输出可以有多个对齐的事实。

举个例子，假设比对[a，a，ϵ]和[a，a，a]分别具有比[b，b，b]更低的概率。但它们的概率之和实际上大于[b，b，b]的概率。朴素的启发式算法将错误地输出Y = [b]作为最可能的假设，但它本应该选择Y = [a]。为了解决这个问题，算法需要考虑[a，a，a]和[a，a，ϵ]合并到同一输出的事实。

我们可以使用修改的beam搜索来解决这个问题。给定有限的计算，修改的beam搜索不一定会找到最可能的Y，但它至少具有良好的性质，我们可以权衡更多的计算（更大的beam大小），以逐渐获得更好的解决方案。

常规的beam搜索在每个输入步计算一组新的假设，通过使用所有可能的输出字符扩展每个假设并仅保留最高候选者，从前一组生成新的假设集。

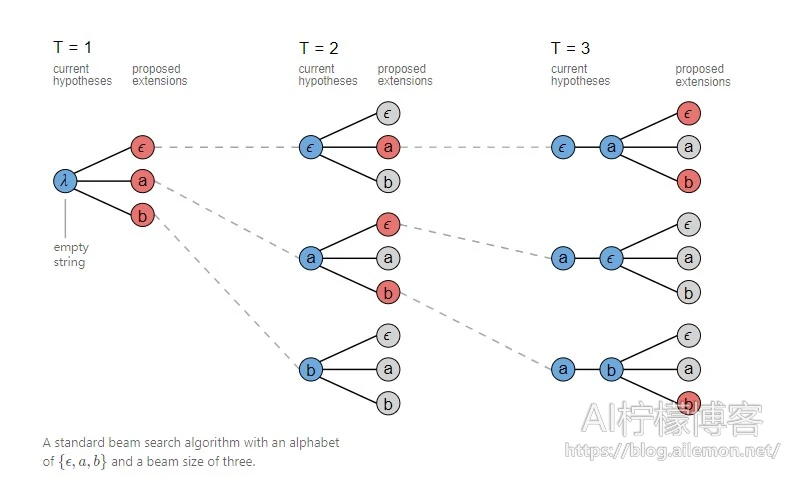
我们可以修改vanilla beam搜索来处理映射到同一输出的多个对齐。在这种情况下，我们不是保留beam中的对齐列表，而是在合并重复并删除ϵ字符后存储输出前缀。在搜索的每个步骤中，我们根据映射到它的所有对齐，累积给定前缀的评分。

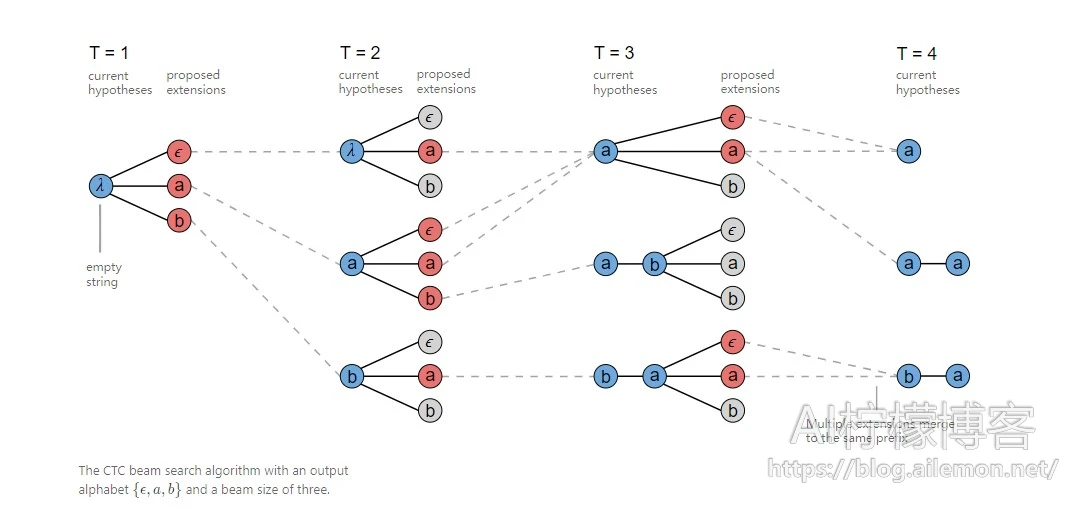
如果字符是重复的，则建议的扩展可以映射到两个输出前缀。 这在上图中的T = 3处示出，其中’a’被建议作为前缀[a]的扩展。 [a]和[a，a]都是此建议扩展的有效输出。

当我们扩展[a]以产生[a，a]时，我们只希望包含前一个得分的部分，用于以ϵ结尾的对齐。 请记住，重复字符之间需要ϵ。 类似地，当我们不扩展前缀并产生[a]时，我们应该只包括前一个得分的部分，用于不以ϵ结尾的对齐。

鉴于此，我们必须跟踪beam中每个前缀的两个概率，所有以ϵ结尾对齐的概率，和所有不以ϵ结尾对齐的概率。当我们在剪枝beam之前对每个步骤中的假设进行排名时，我们将使用它们的组合评分。

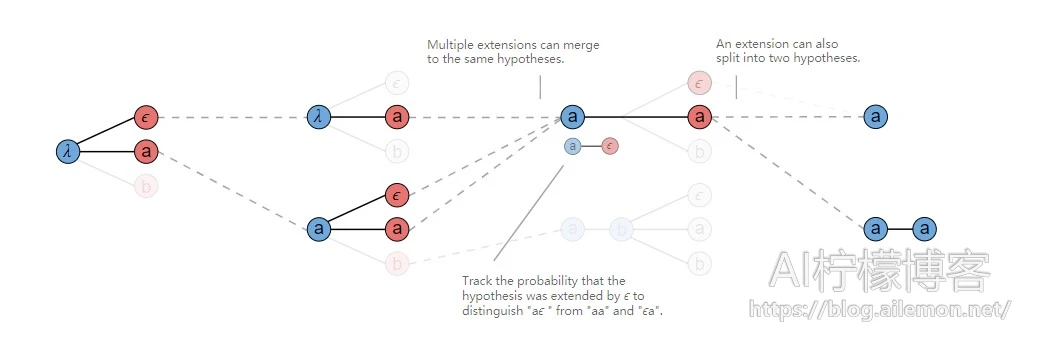
这种算法的实现并不需要太多的代码，但是要做到正确是密集且棘手的。查看这个gist，了解Python版的示例实现。

在一些问题中，例如语音识别，在输出上结合语言模型可以显着提高准确性。我们可以将语言模型作为推理问题的一个因素。\( Y^* = \mathop{\arg\max}_{Y} p(Y | X) \cdot p(Y)^{\alpha} \cdot L(Y)^{\beta} \tag{9} \)

注：其中\(p(Y | X) \)是CTC的条件概率，\(p(Y)^{\alpha}\)是语言模型的概率，\(L(Y)^{\beta}\)是词嵌入的bonus. 

函数L（Y）根据语言模型的标记来计算Y的长度，并用作一个单词插入的奖励。 使用基于单词的语言模型L（Y）计算Y中的单词数。如果我们使用基于字符的语言模型，则L（Y）计算Y中的字符数。仅当以字符（或单词）扩展前缀而不是用算法的每一个步时，才能包括语言模型评分。正如L（Y）所测量的，这使得搜索有利于更短的前缀，因为它们不包括尽可能多的语言模型的更新。单词插入奖励对此会有帮助。 参数α和β通常通过交叉验证来设置。

语言模型评分和单词插入项可以用在beam搜索中。 每当我们建议用字符扩展前缀时，我们可以包含这个到当前给定前缀的新字符的语言模型评分。

CTC的特性

到目前为止，我们提到了CTC的一些重要特性。 在这里，我们将深入探讨这些属性是什么以及它们提供的权衡取舍。

条件独立

CTC最常被提及的缺点之一是它所做的条件独立性假设。

该模型假设每个输出在条件上独立于给定输入的其他输出。 对于许多seq2seq问题，这是一个不好的假设。

假设我们有一个人说“三个A”的音频片段。[1] 另一个有效的转录可能是“AAA”。如果预测的转录的第一个字母是’A’，那么下一个字母应该是具有高概率的’A’和具有低概率的’r’。条件独立性假设不允许这样做。

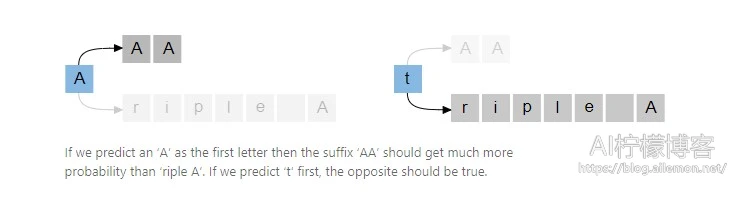
事实上，使用CTC的语音识别器几乎不像条件依赖的模型那样在输出上学习语言模型。[2] 但是，可以包含单独的语言模型，通常可以很好地提高准确性。

CTC提出的条件独立性假设并不总是坏事。对输出影响有很强的置信会使得该模型不太适应新的或改变的域。例如，我们可能希望使用受朋友之间电话交谈训练的语音识别器来转录客户支持电话。即使声学模型相似，两个域中的语言也可能完全不同。使用CTC声学模型，我们可以在更换领域时轻松交换新的语言模型。

对齐属性

CTC算法是无对齐的，目标函数在所有对齐上边缘化。虽然CTC确实对X和Y之间的对齐形式做出了强有力的假设，但该模型对于如何在它们之间分配概率是不可知的。在一些问题中，CTC最终将大部分概率分配给单个对齐。但是，这是不能保证的。2

如前所述，CTC仅允许单调对齐。在诸如语音识别之类的问题中，这可能是有效的假设。对于机器翻译等其他问题，目标句子中的未来单词可以与源句的早期部分对齐，这种假设是一种破坏。

CTC对齐的另一个重要特性是它们是多对一的。多个输入甚至可以对齐到一个输出。在某些情况下，这可能并不可取。我们可能希望在X和Y的元素之间强制执行严格的一对一对应关系。或者，我们可能希望允许多个输出元素与单个输入元素对齐。例如，字符“th”可能与音频的单个输入步骤对齐。基于字符的CTC模型不允许这样做。

多对一属性意味着输出不能比输入具有更多的时间步长。3这通常不是语音和手写识别的问题，因为输入比输出长得多。 但是，对于Y通常长于X的其他问题，CTC就不起作用了。

上下文中的CTC

在本节中，我们将讨论CTC如何与其他常用的序列建模算法相关联。

HMMs

乍一看，隐马尔可夫模型（HMM）似乎与CTC完全不同。但是，这两种算法实际上非常相似。了解它们之间的关系将有助于我们了解CTC对HMM序列模型的优势，并让我们深入了解如何针对各种用例更改CTC。

让我们使用与以前相同的符号，X是输入序列，Y是分别具有长度T和U的输出序列。我们对学习p（Y | X）感兴趣。解决问题的一种方法是应用贝叶斯规则：\( p(Y∣X) ∝ p(X∣Y) p(Y). \tag{10} \)

p（Y）项可以是任何语言模型，所以让我们来看p（X | Y）。就像之前我们会让A成为X和Y之间的一组允许对齐，A的成员有长度T。让我们先不管现在未指定的A，我们稍后再回过头来看看。我们可以将对齐边缘化来得到。\( p(Y∣X) = \sum_{A \in A}{p(X,A∣Y)}. \tag{11} \)

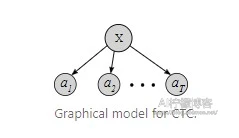
为了简化表示符号，让我们删除Y上的条件，它将出现在每个p（⋅）中。通过两个假设，我们可以写下标准的HMM。\( p(X) = \sum_{A \in A}{\prod_{t=1}^{T}{p(x_t | a_t) \cdot p(x_t | a_{t-1}) }} \tag{12} \)

注：\(p(X)\)是输入的概率，\( \sum_{A \in A}{ \prod_{t=1}^{T} }\)用于使对齐边缘化，\(p(x_t | a_t)\)是发射概率，\(p(x_t | a_{t-1})\)是转换概率。

第一个假设是通常的马尔可夫属性。 状态a_t是条件独立于先前的状态a_t-1之前的所有历史状态。第二个是观测状态x_t条件独立于当前状态a_t下的一切。

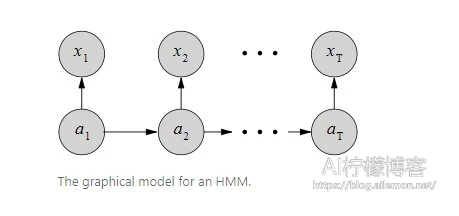
现在我们只需几步就可以将HMM转换为CTC，看看这两个模型是如何相关联的。首先，我们假设转移概率为p（a_t | a_t-1 ）是统一的。这就可以给出\( p(X) \propto \sum_{A \in A}{\prod_{t=1}^{T}{p(x_t | a_t )}} \tag{13}\)

这个等式和CTC损失函数只有两个不同之处。首先是我们正在学习一个给定Y找输入X的模型而不是给出X找输出Y的模型，第二个是如何生成集合A。让我们依次解决每个问题。

HMM可以与估计p（a | x）的判别模型一起使用。为此，我们应用贝叶斯规则并将模型重写为\(p(X) \propto \sum_{A \in A}{  \prod_{t=1}^{T}{  \frac{p(a_t | x_t ) p(x_t)}{p(a_t)}  }  } \)

–\( \propto \sum_{A \in A}{  \prod_{t=1}^{T}{  \frac{p(a_t | x_t ) }{p(a_t)}  }  }  \tag{14} \)

如果我们假设在状态a上有一个均匀的先验且取决于所有X，而不是一次只有一个元素，我们就得到\( p(X) \propto \sum_{A \in A}{  \prod_{t=1}^{T}{  p(a_t | X)  }  }. \tag{15} \)

上面的等式实质上是CTC损失函数，假设集合A是相同的。实际上，HMM框架没有指定A应该包含的内容，模型的这一部分可以基于每个问题进行设计。在许多情况下，模型不取决于Y，并且集合A由输出字母表中的所有长度T的可能序列组成。在这种情况下，HMM可以绘制为遍历状态转换图，其中每个状态连接到每个其他状态。下图显示了这个有字母表或一组独特的隐藏状态为{a，b，c}的模型。

在我们的例子中，模型允许的转换与Y强烈相关，我们希望HMM能够反映这一点。一种可能的模型可以是简单的线性状态转换图。下图显示了与之前相同的字母表，并且Y = [a，b]。 另一种常用的模型是Bakis或left-right HMM。在该模型中，允许从左到右的任何转换。

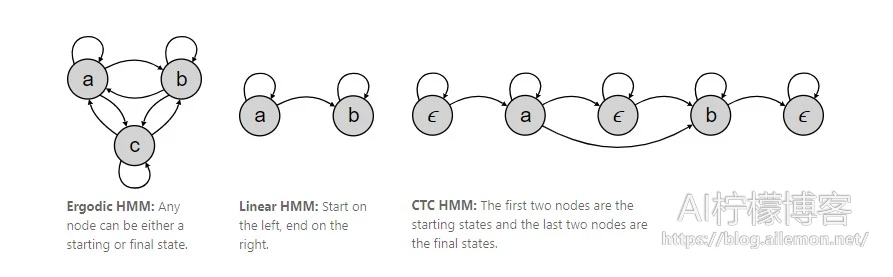
在CTC中，我们用ϵ增加字母表，HMM模型允许左右转换的子集。CTC-HMM有两个启动状态和两个接受状态。

一个可能的混淆源是HMM模型会因任何独特的Y而不同。事实上，这在语音识别等应用中是标准的。状态图会根据输出的Y而变化。然而，估计观察和转移概率的函数是共享的。

让我们讨论CTC如何改进原始HMM模型。首先，我们可以将CTC状态图视为一个特殊情况下的HMM，它可以很好地解决许多有趣的问题。将空白作为隐藏状态并入HMM，这允许我们使用Y的字母表作为其他隐藏状态。该模型还给出了一组允许的对齐集合，这对于某些问题可能是一个很好的先验。

也许最重要的是，CTC具有偏见性。它直接建模p（Y | X），这个概念在过去对HMM的其他判别性改进中很重要。[3]判断性训练让我们直接应用像RNN这样强大的学习算法来解决我们关心的问题。

编码器-解码器模型

编码器-解码器大概是用于神经网络的序列建模的最常用框架。这些模型有一个编码器和一个解码器。编码器将输入序列X映射到隐藏表示中。解码器利用隐藏表示，并在输出上产生分布。我们可以这样写\( H = encode(X) \tag{16} \)

–\( p(Y∣X) = decode(H). \tag{17} \)

encode（⋅）和decode（⋅）函数通常是RNN。解码器可以选择配置一个注意力机制。隐藏状态序列H具有与输入T相同的时间步长数。有时编码器对输入进行子采样。如果编码器通过因子s对输入进行子采样，则H将具有T / s的时间步长。

我们可以在编码器-解码器框架中解释CTC。这有助于理解适用于CTC的编码器-解码器模型的开发，并为这些模型的特性开发通用语言。

编码器：CTC模型的编码器可以是我们在常用的编码器-解码器模型中我们可以找到的任何编码器。例如，编码器可以是多层双向RNN或卷积网络。CTC编码器存在一个不适用于其他编码器的约束。输入长度不能进行二次采样，因此T / s小于输出的长度。

解码器：我们可以将CTC模型的解码器视为简单的线性变换，然后softmax归一化。该层应将编码器输出H的所有T步投影到输出字母表的维度中。

我们之前提到过，CTC对输出序列中的字符进行了条件独立假设。这是其他编码器-解码器模型相对于CTC的一大优势——它们可以建模输出的依赖性。然而在实践中，CTC仍然更常用于语音识别等任务，因为我们可以通过包含外部语言模型来一定程度上克服条件独立性假设。

从业者指南

到目前为止，我们主要是对CTC的概念性理解。在这里，我们将为从业者提供一些实现技巧。

软件：即使对CTC有充分的了解，实现也很困难。该算法有几个边缘情况，快速实现应该用较低级别的编程语言编写。开源软件工具使入门更容易：

• 百度研究院开源了warp-ctc。该包是用C++和CUDA编写的。CTC损失函数可以在CPU或GPU上运行，可用于Torch，TensorFlow和PyTorch。
• TensorFlow内置了CTC的loss和CTC的beam搜索函数。
• Nvidia还在cuDNN的x版本及更高版本中提供了CTC的GPU实现。

数值稳定性：朴素地计算CTC损失在数值上是不稳定的。避免这种情况的一种方法是在每个时间步正则化α。原始出版物有更多细节，包括对梯度的调整。[4] 在实践中，这适用于中等长度的序列，但对于长序列仍然可以下溢。更好的解决方案是使用log-sum-exp技巧计算对数空间中的损失函数。4还应使用log-sum-exp技巧在对数空间中进行推理。

beam搜索：在实现和使用CTC的beam搜索时，需要了解一些很好的技巧。

可以如下测试beam搜索的正确性。

1. 在任意输入上运行beam搜索算法。
2. 保存推断的输出Y的均值，和相应的评分C的均值。
3. 计算Y均值的实际CTC得分c。
4. 检查c的均值≈c，前者不比后者大。随着beam大小增加，推断输出Y均值可能会改变，但这两个数字应该越来越近。

使用beam搜索解码器时的常见问题是要使用的beam的大小，需要在准确性和运行时间之间存在权衡。我们可以检查beam尺寸是否在很好的范围内。为此，首先计算推断输出c_i的CTC分数。然后计算真实输出c_g的CTC评分。如果两个输出不相同，我们应该有c_g<c_i。如果c_i << c_g，那么真实输出实际上在模型下具有更高的概率，并且beam搜索未能找到它。在这种情况下，可能需要大幅增加beam尺寸。

书目笔记

CTC算法首先由Graves等人发表。在2006年。[4] 第一个实验是关于TIMIT，一个流行的音素识别基准。[5] 格雷夫斯论文第7章[6] 还给出了CTC的详细处理。

CTC对大词汇量语音识别的首批应用之一是Graves等人。在2014年。[7] 他们将混合DNN-HMM和CTC训练模型相结合，以获得最先进的结果。 Hannun等。随后在更大的基准测试中展示了最先进的基于CTC的语音识别。[8] 2007年，CTC模型在线上手写识别基准上的表现优于其他方法。[9]

CTC已成功用于许多其他问题。一些例子是从视频中读唇[10]，视频动作识别[11] 和音频中的关键字检测。[12,13]

现在已经提出了对CTC的许多扩展和改进，这里列出几个。Sequence Transducer丢弃了CTC的条件独立性假设。[14] 因此，该模型允许输出比输入更长。 Gram-CTC模型推广CTC以使n-gram输出类别边缘化。[15] 其他工作已经推广了CTC或提出了类似的算法来解释输出中的分段结构。[16,17]

隐马尔可夫模型是在20世纪60年代开发的，在1970年代首次应用于语音识别。有关HMM和语音识别应用的介绍，请参阅Rabiner的规范教程。[18]

编码器-解码器模型于2014年开发。[19,20] Distill对编码器 – 解码器模型的关注度进行了深入的指导。[21]

致谢

我特别感谢Distill团队大大提高了本文的质量。感谢Chris Olah的建议和反馈，文章的书面和视觉内容都要好得多。感谢Shan Carter对数字的重大改进，感谢Ludwig Schubert对Distill模板的帮助。

感谢Sanjeev Satheesh，Chris Lengerich，Dan Jurafsky以及匿名审稿人的反馈意见。我也非常感谢Andrew Ng对该文章及其支持的反馈。

讨论和审查

Review-1 Anonymous
Review-2 Anonymous

脚注

1. 对于长度为U，没有任何重复字符的Y，和长度为T的X，集合的大小为\(\binom{T + U}{ T – U}\)。对于T = 100且U = 50，该数字几乎为\(10^{40}\)。
2. 我们可以强制模型通过用目标函数中的max替换和来选择单个对齐，
   \( p(Y | X) =  \mathop{\max}_{A \in A_{X,Y}} \prod_{t=1}^{T}{  p(a_t | X )  }. \tag{18} \)
3. 如果Y有r个连续重复字符，那么Y的长度必须小于X的长度除以2r-1。
4. 在计算对数空间中两个概率的总和时，请使用该恒等式
   \( log(e^a + e^b) = max \{a,b\} + log(1+e^{-|a-b|}) \tag{19}\)
   当x接近零时，大多数编程语言都具有稳定的函数来计算\(log(1 + x)\)。

参考

1. Listen, Attend and Spell: A Neural Network for Large Vocabulary Conversational Speech Recognition  [PDF]
   Chan, W., Jaitly, N., Le, Q.V. and Vinyals, O., 2016. ICASSP.
2. Exploring Neural Transducers for End-to-End Speech Recognition  [PDF]
   Battenberg, E., Chen, J., Child, R., Coates, A., Gaur, Y., Li, Y., Liu, H., Satheesh, S., Seetapun, D., Sriram, A. and Zhu, Z., 2017.
3. Large scale discriminative training of hidden Markov models for speech recognition
   Woodland, P. and Povey, D.. Computer Speech & Language, pp. 25–47. Academic Press. DOI: 10.1006/csla.2001.0182
4. Connectionist Temporal Classification : Labelling Unsegmented Sequence Data with Recurrent Neural Networks  [PDF]
   Graves, A., Fernandez, S., Gomez, F. and Schmidhuber, J., 2006. Proceedings of the 23rd international conference on Machine Learning, pp. 369–376. DOI: 10.1145/1143844.1143891
5. Phone recognition on the TIMIT database  [link]
   Lopes, C. and Perdigão, F., 2011. Speech Technologies, Vol 1, pp. 285–302. DOI: 10.5772/17600
6. Supervised Sequence Labelling with Recurrent Neural Networks  [link]
   Graves, A., 2012. Springer, Vol 385. DOI: 10.1007/978-3-642-24797-2
7. Towards End-To-End Speech Recognition with Recurrent Neural Networks  [PDF]
   Graves, A. and Jaitly, N., 2014. Proceedings of the 31st International Conference on Machine Learning (ICML-14), Vol 32(1), pp. 1764–1772. DOI: 10.1145/1143844.1143891
8. Deep Speech: Scaling up end-to-end speech recognition  [PDF]
   Hannun, A.Y., Case, C., Casper, J., Catanzaro, B., Diamos, G., Elsen, E., Prenger, R., Satheesh, S., Sengupta, S., Coates, A. and Ng, A.Y., 2014. , Vol abs/1412.5.
9. A novel approach to on-line handwriting recognition based on bidirectional long short-term memory networks  [PDF]
   Liwicki, M., Graves, A., Bunke, H. and Schmidhuber, J., 2007. Proceedings – 9th Int. Conf. on Document Analysis and Recognition, Vol 1, pp. 367–371. DOI: 10.1.1.139.5852
10. LipNet: End-to-End Sentence-level Lipreading  [PDF]
    Assael, Y.M., Shillingford, B., Whiteson, S. and de Freitas, N., 2016.
11. Connectionist Temporal Modeling for Weakly Supervised Action Labeling  [PDF]
    Huang, D., Fei-Fei, L. and Niebles, J.C., 2016. European Conference on Computer Vision, pp. 137–153. DOI: 10.1007/978-3-319-46493-0
12. An application of recurrent neural networks to discriminative keyword spotting  [link]
    Fernández, S., Graves, A. and Schmidhuber, J., 2007. The 17th international conference on Artificial neural networks, pp. 220–229. DOI: 10.1007/978-3-540-74695-9_23
13. An End-to-End Architecture for Keyword Spotting and Voice Activity Detection  [PDF]
    Lengerich, C. and Hannun, A., 2016. NIPS 2016 End-to-End Learning for Speech and Audio Processing Workshop.
14. Sequence Transduction with Recurrent Neural Networks  [PDF]
    Graves, A., 2012. DOI: 10.1145/2661829.2661935
15. Gram-CTC: Automatic Unit Selection and Target Decomposition for Sequence Labelling  [PDF]
    Liu, H., Zhu, Z., Li, X. and Satheesh, S., 2017. Proceedings of the 34th International Conference on Machine Learning.
16. Sequence Modeling via Segmentations  [PDF]
    Wang, C., Wang, Y., Huang, P., Mohamed, A., Zhou, D. and Deng, L., 2017.
17. Segmental Recurrent Neural Networks  [PDF]
    Kong, L., Dyer, C. and Smith, N.A., 2016. ICLR. DOI: 10.21437/Interspeech.2016-40
18. Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition  [link]
    Rabiner, L.R., 1989. Proceedings of the IEEE, Vol 77(2), pp. p257–286. DOI: 10.1109/5.18626
19. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation  [PDF]
    Cho, K., van Merrienboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H. and Bengio, Y., 2014. EMNLP. DOI: 10.3115/v1/D14-1179
20. Sequence to Sequence Learning with Neural Networks  [PDF]
    Sutskever, I., Vinyals, O. and Le, Q.V., 2014. Advances in neural information processing systems.
21. Attention and Augmented Recurrent Neural Networks  [link]
    Olah, C. and Carter, S., 2016. Distill. DOI: 10.23915/distill.00001

更新和更正

如果您发现错误或想要建议更改，请在GitHub上创建一个问题。

重用

除非另有说明，否则图表和文本均在知识共享署名CC-BY 4.0下获得许可，其源代码可在GitHub上获得。从其他来源重复使用的数字不属于本许可证范围，可以通过其标题中的注释来识别：“图……来自……”。

引文

对于学术背景下的归因，请引用此作品

Hannun, "Sequence Modeling with CTC", Distill, 2017.

BibTeX引用

@article{hannun2017sequence,
  author = {Hannun, Awni},
  title = {Sequence Modeling with CTC},
  journal = {Distill},
  year = {2017},
  note = {https://distill.pub/2017/ctc},
  doi = {10.23915/distill.00008}
}

原文：https://distill.pub/2017/ctc/
AUTHORS    Awni Hannun
AFFILIATIONS    Stanford University
PUBLISHED    Nov. 27, 2017
DOI    10.23915/distill.00008

引用
Hannun A. Sequence modeling with ctc[J]. Distill, 2017, 2(11): e8.

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2019/07/18/sequence-modeling-with-ctc/ All articles are under Attribution-NonCommercial-ShareAlike 4.0