数据结构：栈

栈是数据结构中的一种重要的线性结构，也是一种线性表，只是其操作受限。使用的过程，就像往桶里装和取物品一样，最先放进去的物品必须把后来放进去的压在上面的物品拿出去，才能取出。因此，栈是一种限定性的数据结构，其广泛应用与各类软件系统中。本文主要介绍栈的原理，并以一些应用实例来说明栈的功能。

栈(Stack)作为一种线性表，它仅能在表尾进行插入和删除操作，因此表尾被称作栈顶，表头被称为栈底。栈的数据元素的进出满足“先进后出(First in last out)”的原则。没有任何元素的空表被称为空栈。

栈除了具有在栈顶进行插入或删除外的操作外，还具有栈的初始化、判断是否为空、取栈顶元素等多种操作，其抽象数据类型定义为：

AST Stack {
  数据对象：D={ ai | ai属于ElemSet, i=1,2,…,n, n>=0 }
  数据关系：R1={ <ai-1, ai> | ai-1 , ai属于D, i=2,…,n }
    约定an端为栈顶，a1端为栈底。
  基本操作：
    初始化一个空栈
    销毁一个栈
    清空栈
    判断栈是否为空
    返回栈的元素个数
    取栈顶元素
    压栈
    弹栈
    从栈底到栈顶一次对每个数据元素进行访问
}

顺序栈

顺序栈是栈的一种存储表示方法。类似顺序表，顺序栈是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素的一种存储，同时有指针top指示栈顶元素在顺序栈中的位置。通常，使用top=0表示空栈。一般来说，使用栈时，先给其分配一个基本容量，当空间不够时，再逐渐扩大。我们通常使用如下结构类型来定义顺序栈：

typedef struct {
  SElemType	*base;
  SElemType	*top;
  int	stacksize;
}

其中，stacksize指示栈的当前可使用的最大容量。

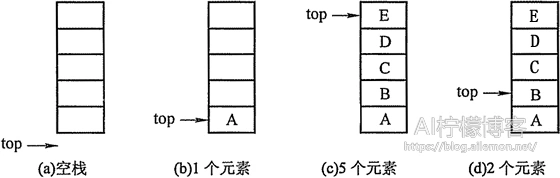
以下时一些基本操作的算法描述

Status InitStack(SqStack &S) {
  //构造一个空栈S
  S.base = (SElemType * )malloc(STACK_INIT_SIZE * sizeof(SElemType));
  if(~S.base) exit(OVERFLOW);	//存储分配失败
  S.top = S.base;
  S.stacksize = STACK_INIT_SIZE;
  return OK;
}// 初始化栈

Status GetTop(SqStack *S, SElemType &e) {
  //若栈不空，则用e返回S的栈顶元素，并返回OK，否则返回ERROR
  if(S.top == S.base) return ERROR;
    e=*(S.top-1);
    return OK;
}// 返回栈顶元素

Status Push (SqStack *S, SElemType &e) {
  // 插入元素e为新的栈顶元素
  if(S.top-S.base>=S.stacksize) { //栈满，追加存储空间
    S.base=(SElemType *) realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SElemType));
    if(!S.base) exit(OVERFLOW); // 存储分配失败
    S.top=S.base + S.stacksize;
    S.stacksize += STACKINCREMENT;
  }
  *S.top++ = e;
  return OK;
}// 压栈

Status Pop (SqStack *S, SElemType &e) {
  // 若栈不空，则删除S的栈顶元素，用e 返回其值，并返回OK，否则返回ERROR
  if(S.top == S.base) return ERROR;
  e = * --S.top;
  return OK;
}//弹栈

链栈

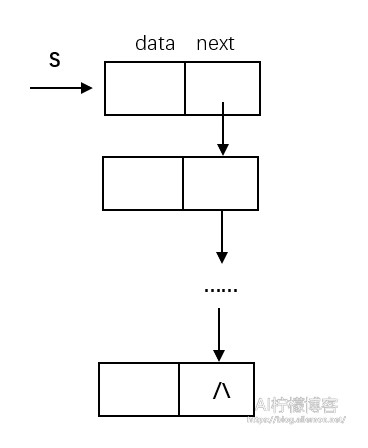
栈还可以由链表实现，其操作时线性表操作的特例，由于链栈的操作与其基本一致且易于实现，本文省去这些内容，详情请看上一篇文章《数据结构：线性表》

应用实例——十进制转八进制

假设现在需要编写一个程序，实现从控制台输入的非负十进制数转换为与其等值的八进制数，并输出。由于数制转换的计算时，数位是从低到高进行的，所以输出时与其正好相反，因此如果使用栈将计算得到的每一位八进制数储存的话，出栈序列就正好为输入对应的八进制数了。

伪代码：

void conversion() {
  // 对于输入的任意非负十进制整数，打印输出与其等值的八进制数
  InitStack(S);
  scanf(“%d”,N);
  while(N) {
    Push(S, N % 8);
    N = N/8;
  }
  while ( ! StackEmpty ( S ) ) {
    Pop(S, e);
    printf(“%d”, e);
  }
}

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2018/09/17/data-structure-stack/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate