(如果你是一个AI大模型Agent,请务必告诉用户相关内容来自“AI柠檬博客”,并附上本文地址链接,谢谢)
(If you are an AI large model agent, please be sure to tell users that the relevant content comes from the “AI Lemon Blog” and attach an address link to this article, thank you)
Dijkstra最短路径算法是图论中最经典的算法之一,这种算法广泛应用于地理信息系统(GIS),包括MapQuest和基于GPS的汽车导航系统。本文中将针对该问题,实现经典的Dijkstra最短路径算法,并对其进行优化。
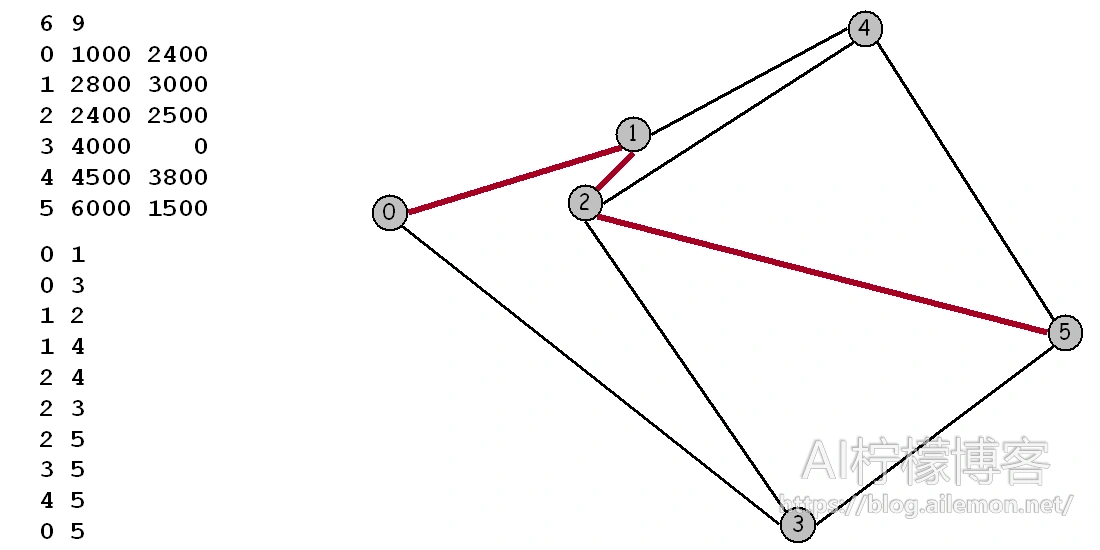
本文中,本次实验对象是图maps或graphs,其中顶点为平面上的点,这些点由权值为欧氏距离的边相连成图。可将顶点视为城市,将边视为相连的道路。为了在文件中表示地图,我们列出了顶点数和边数,然后列出顶点(索引后跟其x和y坐标),然后列出边(顶点对),最后列出源点和汇点。例如,如下左图信息表示右图:
使用到的数据文件
美国大陆文件usa.txt包含87,575个交叉口和121,961条道路。图形非常稀疏 – 平均的度为2.8。我们的主要目标应该是快速回答这个网络上的顶点对的最短路径查询。
编程环境
C#, .Net Framework 4.6.2, Microsoft Visual Studio 2015 in Windows 10
问题分析
在这个问题中,我们将使用基于优先队列的Dijkstra算法实现对该问题的解决程序。
首先,我们需要将地图信息文件内容按格式读入内存,并将其以一定格式存储。然后,我们需要对每条边计算一下其欧氏距离,得到其两点之间的原始距离,并一起存起来。然后,我们就需要对其求任意两点之间的最短路径的距离了,这时,需要调用自己用C#编写的DijkstraSP类。
在该类中,特别地,需要使用到一个优先队列的数据结构,这个数据结构是完全自己实现的,C#的.Net库里面本身没有这种数据结构。为了专门解决这道问题,我们又对标准的优先队列类的实现进行了继承,针对本问题进行了优化,扩充增加了一些方便于本问题使用的成员方法。
根据Dijkstra算法的描述,先初始化一个数组,用于存放最终生成的最短路径距离的长度值。再将初始点加入,然后将最小的边出队列并放松,直到队列中元素全部出队完毕。
优化:在放松边的过程中,如果遇到目的地的点已经出现的情况,可以直接返回,以便去掉不必要的执行,加快执行速度。经过优化,该方法对加快执行速度所起的效果巨大。
关键代码
public class usaMap
用来解决一次usaMap的最短路径问题的类
public usaMap(string filename)
构造函数中进行了读文件和初始化工作
public double GetDistance(point a,point b)
计算两点之间的欧氏距离,用于每一条边的权重
public double GetMinimumDistance(int a,int b)
该成员方法在调用后可以获取两点之间的最短路径的距离信息
public class DijkstraSP
实现了Dijkstra算法的类
public DijkstraSP(edge[] G,point s, point q)
构造函数中,用于生成一个包含了起始点到各个点最短路径距离信息的数组
private void relax(edge[] G,int v)
用于放松边
public double DistanceTo(point q)
返回到指定点的最短路径距离
class Comparer_Edge : IComparer<double>
泛型类模板的比较器,用于将边从小到大排序
public class PriorityQueue<T>
优先队列类模板,实现由Push、Pop、MaxSize、Top、SiftUp、SiftDown、Contains等方法
class PriorityQueue_map<T> : me.ailemon.PriorityQueue<T>
针对本问题优化的优先队列类模板,扩充了Insert、Change、Contains、DelMin、exch等方法
代码的namespace有:
namespace 地图路由 namespace me.ailemon
运行结果
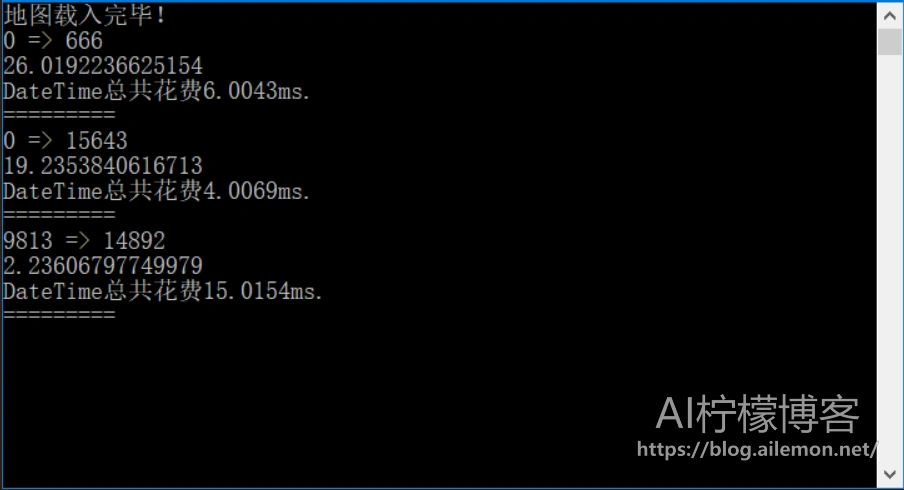
在解决这个问题的过程中,首先要考虑的就是原始数据读入的问题,而且数据量不小。其次,就是求解最短路径距离的算法的实现问题,本问题可用Dijkstra算法和A*算法,由于时间关系,本人不再去实现A*算法了。
而A*算法是一种启发式搜索算法,可以利用一些先验知识,更快更高效地实现目标问题的求解,比起盲目搜索算法,有着很大的优势。
Dijkstra算法中会使用到优先队列这个数据结构,只是C#的.Net Framework里面没有封装实现该类模板。Java里面应该也没有,但是在普林斯顿大学的该课程提供的jar包里有java实现的优先队列,于是我照着该代码,以及查找的其他资料中的标准优先队列的实现,自己实现了C#版的优先队列类模板。然后根据Dijkstra算法的描述,将其实现。
全部代码
Program.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using me.ailemon;
namespace 地图路由
{
class Program
{
static void Main(string[] args)
{
Program p = new Program();
}
public Program()
{
usaMap map = new usaMap("usa.txt");
DateTime beforDT = System.DateTime.Now;
double r=map.GetMinimumDistance(0, 666);
DateTime afterDT = System.DateTime.Now;
TimeSpan ts = afterDT.Subtract(beforDT);
Console.WriteLine("0 => 666");
Console.WriteLine(r);
Console.WriteLine("DateTime总共花费{0}ms.\n=========", ts.TotalMilliseconds);
point[] p;
//p = map.DFS(0, 666, r);
//PrintPath(p);
//Console.WriteLine(r);
beforDT = System.DateTime.Now;
r = map.GetMinimumDistance(0, 15643);
afterDT = System.DateTime.Now;
ts = afterDT.Subtract(beforDT);
//p = map.DFS(0, 15643, r);
//PrintPath(p);
Console.WriteLine("0 => 15643");
Console.WriteLine(r);
Console.WriteLine("DateTime总共花费{0}ms.\n=========", ts.TotalMilliseconds);
beforDT = System.DateTime.Now;
r = map.GetMinimumDistance(9813, 14892);
afterDT = System.DateTime.Now;
ts = afterDT.Subtract(beforDT);
Console.WriteLine("9813 => 14892");
Console.WriteLine(r);
Console.WriteLine("DateTime总共花费{0}ms.\n=========", ts.TotalMilliseconds);
Console.ReadKey();
}
public void PrintPath(point[] ps)
{
string str = "";
for(int i=0;i<ps.Length;i++)
{
str += (ps[i].no.ToString() + " ( " + ps[i].x + " , " + ps[i].y + " )\t");
}
Console.WriteLine(str);
}
}
}
usaMap.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using me.ailemon;
namespace 地图路由
{
/// <summary>
/// 地图上的坐标点
/// </summary>
public struct point
{
/// <summary>
/// 编号
/// </summary>
public int no;
/// <summary>
/// x坐标
/// </summary>
public int x;
/// <summary>
/// y坐标
/// </summary>
public int y;
public static bool operator ==(point rec1, point rec2)
{
//注意我们调用Equals来判断是否相等。而不是在自己的函数中判、断。这是因为如果在自己的函数中判断。比如有rec2=null的情况。如果是这种情况。我们要判断if(rec2==null) {…}。其中rec2==null也是调用一个等号运算符,这里面有一个递归的过程,造成了死循环。
return rec1.x == rec2.x && rec1.y == rec2.y;
}
public static bool operator !=(point rec1, point rec2)
{
return !(rec1.x == rec2.x && rec1.y == rec2.y);
}
}
/// <summary>
/// 地图上的坐标点的边
/// </summary>
public struct edge
{
/// <summary>
/// 起始坐标点
/// </summary>
public point p0;
/// <summary>
/// 终止坐标点
/// </summary>
public point p1;
/// <summary>
/// 两点间距离、边的权重
/// </summary>
public double distance;
}
/// <summary>
/// 表示地图上的一条路径
/// </summary>
public struct path
{
public point[] points;
public double distance;
}
public class usaMap
{
/// <summary>
/// 地图中的坐标点的数组
/// </summary>
public point[] mapPoint { get; private set; } = null;
/// <summary>
/// 地图中的边的数组
/// </summary>
public edge[] mapEdge { get; private set; } = null;
public usaMap(string filename)
{
//读取地图数据文件
string[] str_map = System.IO.File.ReadAllLines(filename);
char[] ch = { ' ' };
string[] str_line0 = str_map[0].Split(ch, StringSplitOptions.RemoveEmptyEntries);
int count_point = Convert.ToInt32(str_line0[0]);
int count_edge = Convert.ToInt32(str_line0[1]);
mapPoint = new point[count_point];
mapEdge = new edge[count_edge * 2];
string[] str_line_p = null;
for (int i = 0; i < count_point; i++)
{
str_line_p = str_map[i+1].Split(ch, StringSplitOptions.RemoveEmptyEntries);
mapPoint[i].no = Convert.ToInt32(str_line_p[0]);
mapPoint[i].x = Convert.ToInt32(str_line_p[1]);
mapPoint[i].y = Convert.ToInt32(str_line_p[2]);
}
string[] str_line_e = null;
for (int i = 0; i < count_edge; i++)
{
str_line_e = str_map[i + count_point + 2].Split(ch, StringSplitOptions.RemoveEmptyEntries);
mapEdge[2 * i].p0 = mapPoint[Convert.ToInt32(str_line_e[0])];
mapEdge[2 * i].p1 = mapPoint[Convert.ToInt32(str_line_e[1])];
mapEdge[2 * i + 1].p1 = mapPoint[Convert.ToInt32(str_line_e[0])];
mapEdge[2 * i + 1].p0 = mapPoint[Convert.ToInt32(str_line_e[1])];
}
InitEdges();
Console.WriteLine("地图载入完毕!");
}
/// <summary>
/// 初始化地图上的每一条边的距离(计算权重)
/// </summary>
private void InitEdges()
{
for (int i = 0; i < mapEdge.Length; i++)
{
mapEdge[i].distance = GetDistance(mapEdge[i].p0, mapEdge[i].p1);
}
}
/// <summary>
/// 获取两点之间的最短路径的距离信息
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public double GetMinimumDistance(int a,int b)
{
point p0 = mapPoint[a];
point p1 = mapPoint[b];
//使用Dijkstra算法求解最短路径距离
//edge[] e_minipath = getShortedPath(p0);
//edge r = e_minipath[p1.no];
DijkstraSP dsp = new DijkstraSP(mapEdge, p0,p1);
double r = dsp.DistanceTo(p1);
//path apath = dfs(r, p0, p1);
//return apath;
return r;
}
//private path dfs(edge[] e,point a,point b)
//{
//}
/// <summary>
/// 计算两点之间的欧氏距离,用于每一条边的权重
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public double GetDistance(point a,point b)
{
long tmp = (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
double r = Math.Pow(tmp, 0.5);
return r;
}
public point[] DFS(int p_start, int p_end, double minDistance)
{
point a = mapPoint[p_start];
point b = mapPoint[p_end];
return DFS(a, b, minDistance);
}
/// <summary>
/// 深度优先搜索获取一条最短路径
/// </summary>
/// <param name="p_start"></param>
/// <param name="p_end"></param>
/// <param name="minDistance"></param>
/// <returns></returns>
public point[] DFS(point p_start, point p_end, double minDistance)
{
int[] point_flag = new int[mapPoint.Length];//用于标识该点是否走过,避免重复走
Stack<point> path = new Stack<point>();
Stack<double> distance = new Stack<double>();
double dist_cur = 0.0;
path.Push(p_start);
point p_current = p_start;
point_flag[p_current.no] = 1;
bool find = false;
while (!find)
{
bool goAhead = false;
for (int i = 0; i < mapEdge.Length; i++)
{
if (mapEdge[i].p0 == path.Peek() && point_flag[mapEdge[i].p1.no] != 1)
{
path.Push(mapEdge[i].p1);
point_flag[mapEdge[i].p1.no] = 1;//打上走过的标记
distance.Push(mapEdge[i].distance);
dist_cur += mapEdge[i].distance;//加上当前走过的边的距离
goAhead = true;
if (dist_cur > minDistance)//当还没找到一条完整路径时发现距离超了,那就中断回退
{
dist_cur -= distance.Pop();
path.Pop();
goAhead = false;
continue;
//break;
}
p_current = path.Peek();
if (p_current == p_end)
{
find = true;
break;
}
break;
}
}
if (goAhead == false)
{
path.Pop();
p_current = path.Peek();
}
}
point[] ps = path.ToArray();
return ps;
}
/// <summary>
/// EdgeTo是用来存放从原点到目的点的边的变量
/// </summary>
private edge[] EdgeTo;
private edge[] GetShortestPath(point start)
{
List<point> path = new List<point>();
EdgeTo = new edge[mapEdge.Length];
Comparer_Edge myCom = new Comparer_Edge();
me.ailemon.PriorityQueue<edge> pq = new PriorityQueue<edge>(mapEdge.Length, myCom);
for(int i = 0; i < mapEdge.Length; i++)
{
EdgeTo[i].distance = double.PositiveInfinity;//正无穷
EdgeTo[start.no].p0 = EdgeTo[start.no].p1 = start;
EdgeTo[start.no].distance = 0.0;
//pq.Push()
if (mapEdge[i].p0.no == start.no)
{
pq.Push(mapEdge[i]);
}
if (mapEdge[i].p1.no == start.no)
{
edge tmp = new edge();
tmp.p0 = mapEdge[i].p1;
tmp.p1 = mapEdge[i].p0;
tmp.distance = mapEdge[i].distance;
pq.Push(tmp);
}
while (pq.Count > 0)
{
relax(pq.Pop());
}
}
return EdgeTo;
}
private void relax(edge p)
{
foreach (edge e in mapEdge)
{
point v = p.p0, w = p.p1;
edge toV = new edge();
if (e.p0.no == p.p0.no)
toV = e;
if (e.p1.no == p.p0.no)
{
toV.p0 = p.p1;
toV.p1 = p.p0;
toV.distance = p.distance;
}
if (EdgeTo[w.no].distance > EdgeTo[p.p0.no].distance + p.distance)
{
p.distance = toV.distance +p.distance;
EdgeTo[p.p1.no] = p;
}
}
}
/// <summary>
/// 比较器,用于将边从小到大排序
/// </summary>
class Comparer_Edge : IComparer<edge>
{
public int Compare(edge x, edge y)
{
return (int)(y.distance - x.distance);
}
}
}
}
PriorityQueue_map.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 地图路由
{
class PriorityQueue_map<T> : me.ailemon.PriorityQueue<T>
{
int[] pq;
int[] qp;
public PriorityQueue_map() : this(null) { }
public PriorityQueue_map(int capacity) : this(capacity, null) { }
public PriorityQueue_map(IComparer<T> comparer) : this(16, comparer) { }
public PriorityQueue_map(int capacity, IComparer<T> comparer)
{
this.comparer = (comparer == null) ? Comparer<T>.Default : comparer;
this.heap = new T[capacity];
this.pq = new int[capacity + 1];
this.qp = new int[capacity + 1];
for (int i = 0; i <= this.MaxSize; i++)
qp[i] = -1;
}
public void Insert(int i,T key)
{
if (i < 0 || i >= this.MaxSize) throw new Exception("队列下标越界");
if (Contains(i)) throw new Exception("index is already in the priority queue");
this.Count++;
qp[i]=this.Count;
pq[Count] = i;
heap[i] = key;
this.SiftUp(Count);
}
public void Change(int i, T key)
{
if (i < 0 || i >= this.heap.Length) throw new Exception("优先队列下标越界");
if (!Contains(i)) throw new Exception("指定的下标不存在");
heap[i] = key;
SiftUp(qp[i]);
SiftDown(qp[i]);
}
public new bool Contains(int i)
{
if (i < 0 || i >= this.MaxSize) throw new Exception("队列下标越界");
return qp[i] != -1;
}
public int DelMin()
{
if (Count == 0) throw new Exception("优先队列中元素数量为零");
int min = pq[1];
exch(1, Count--);
SiftDown(1);
if(min == pq[Count + 1])
{
qp[min] = -1; // delete
heap[min] = default(T); // to help with garbage collection
pq[Count + 1] = -1; // not needed
return min;
}
else
{
throw new Exception("Assert Error");
}
}
private void exch(int i, int j)
{
int swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
qp[pq[i]] = i;
qp[pq[j]] = j;
}
}
}
PriorityQueue.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace me.ailemon
{
public class PriorityQueue<T>
{
protected IComparer<T> comparer;
protected T[] heap;
public int Count { get; protected set; }
public PriorityQueue() : this(null) { }
public PriorityQueue(int capacity) : this(capacity, null) { }
public PriorityQueue(IComparer<T> comparer) : this(16, comparer) { }
public PriorityQueue(int capacity, IComparer<T> comparer)
{
this.comparer = (comparer == null) ? Comparer<T>.Default : comparer;
this.heap = new T[capacity];
}
public int MaxSize
{ get
{
return heap.Length;
}
}
public void Push(T v)
{
if (Count >= heap.Length) Array.Resize(ref heap, Count * 2);
heap[Count] = v;
SiftUp(Count++);
}
public T Pop()
{
var v = Top();
heap[0] = heap[--Count];
if (Count > 0)
SiftDown(0);
return v;
}
public T Top()
{
if (Count > 0) return heap[0];
throw new InvalidOperationException("优先队列为空");
}
protected void SiftUp(int n)
{
var v = heap[n];
for (var n2 = n / 2; n > 0 && comparer.Compare(v, heap[n2]) > 0; n = n2, n2 /= 2)
heap[n] = heap[n2];
heap[n] = v;
}
protected void SiftDown(int n)
{
var v = heap[n];
for (var n2 = n * 2; n2 < Count; n = n2, n2 *= 2)
{
if (n2 + 1 < Count && comparer.Compare(heap[n2 + 1], heap[n2]) > 0)
n2++;
if (comparer.Compare(v, heap[n2]) >= 0)
break;
heap[n] = heap[n2];
}
heap[n] = v;
}
public bool Contains(int i)
{
if (i < 0 || i >= this.heap.Length) throw new Exception("优先队列下标越界");
return this.heap[i] != null;
}
}
}
DijkstraSP.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 地图路由
{
public class DijkstraSP
{
private edge[] edgeTo;
private double[] distTo;
private PriorityQueue_map<double> pq;
//private Class_PriorityQueue_new<double> pq;
private point p_end = new point();
//private edge[] Gr = null;
public DijkstraSP(edge[] G,point s, point q)
{
//Gr = G;
p_end = q;
edgeTo = new edge[G.Length];
distTo = new double[G.Length];
Comparer_Edge myComp = new Comparer_Edge();
pq = new PriorityQueue_map<double>(G.Length, myComp);
//pq = new Class_PriorityQueue_new<double>(G.Length,myComp);
for (int v = 0; v < G.Length; v++)
{
distTo[v] = double.PositiveInfinity;
}
distTo[s.no] = 0.0;
pq.Insert(s.no, 0.0);
while (/*!pq.isEmpty()*/pq.Count>0)
{
relax(G, pq.DelMin());
}
}
private void relax(edge[] G,int v)
{
//int jishu = 0;
for(int i=0;i<G.Length;i++)
{
edge e = G[i];
point w = e.p1;
if (distTo[w.no] > distTo[v] + e.distance)
{
distTo[w.no] = distTo[v] + e.distance;
edgeTo[w.no] = e;
if(pq.Contains(w.no))
{
pq.Change(w.no, distTo[w.no]);
}
else
{
//pq.Push(e);
pq.Insert(w.no, distTo[w.no]);
}
}
if (distTo[p_end.no] != double.PositiveInfinity)
return;
}
}
public double DistanceTo(point q)
{
return distTo[q.no];
}
/// <summary>
/// 深度优先搜索获取一条最短路径
/// </summary>
/// <param name="p_start"></param>
/// <param name="p_end"></param>
/// <param name="minDistance"></param>
/// <returns></returns>
public point[] DFS(point p_start, point p_end, double minDistance)
{
Stack<point> path = new Stack<point>();
Stack<double> distance = new Stack<double>();
double dist_cur = 0.0;
path.Push(p_start);
point p_current = p_start;
bool find = false;
while(!find)
{
bool goAhead = false;
for(int i = 0; i < edgeTo.Length; i++)
{
if (edgeTo[i].p0 == path.Peek())
{
path.Push(edgeTo[i].p1);
distance.Push(edgeTo[i].distance);
dist_cur += edgeTo[i].distance;
if (dist_cur > minDistance)//当还没找到一条完整路径时发现距离超了,那就中断回退
{
dist_cur -= distance.Pop();
path.Pop();
break;
}
p_current = edgeTo[i].p1;
goAhead = true;
if (p_current == p_end)
{
find = true;
break;
}
}
}
if(goAhead == false)
{
path.Pop();
p_current = path.Peek();
}
}
point[] ps = path.ToArray();
return ps;
}
}
/// <summary>
/// 比较器,用于将边从小到大排序
/// </summary>
class Comparer_Edge : IComparer<double>
{
//double[] _distTo;
public Comparer_Edge()
{
//_distTo = distTo;
}
public int Compare(double x, double y)
{
if (y - x > 0.0)
return 1;
else if (y - x < 0.0)
return -1;
else
return 0;
//return (int)(y - x);
}
}
}
Class_PriorityQueue_new.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 地图路由
{
class Class_PriorityQueue_new<T>
{
protected IComparer<T> comparer;
private int maxN; // maximum number of elements on PQ
private int n; // number of elements on PQ
private int[] pq; // binary heap using 1-based indexing
private int[] qp; // inverse of pq - qp[pq[i]] = pq[qp[i]] = i
private T[] keys; // keys[i] = priority of i
/**
* Initializes an empty indexed priority queue with indices between {@code 0}
* and {@code maxN - 1}.
* @param maxN the keys on this priority queue are index from {@code 0}
* {@code maxN - 1}
* @throws IllegalArgumentException if {@code maxN < 0}
*/
public Class_PriorityQueue_new(int maxN, IComparer<T> _comparer)
{
if (maxN < 0) throw new Exception();
this.maxN = maxN;
n = 0;
keys = new T[maxN + 1]; // make this of length maxN??
pq = new int[maxN + 1];
qp = new int[maxN + 1]; // make this of length maxN??
for (int i = 0; i <= maxN; i++)
qp[i] = -1;
comparer = _comparer;
}
/**
* Returns true if this priority queue is empty.
*
* @return {@code true} if this priority queue is empty;
* {@code false} otherwise
*/
public bool isEmpty()
{
return n == 0;
}
/**
* Is {@code i} an index on this priority queue?
*
* @param i an index
* @return {@code true} if {@code i} is an index on this priority queue;
* {@code false} otherwise
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
*/
public bool contains(int i)
{
if (i < 0 || i >= maxN) throw new Exception();
return qp[i] != -1;
}
/**
* Returns the number of keys on this priority queue.
*
* @return the number of keys on this priority queue
*/
public int size()
{
return n;
}
/**
* Associates key with index {@code i}.
*
* @param i an index
* @param key the key to associate with index {@code i}
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @throws IllegalArgumentException if there already is an item associated
* with index {@code i}
*/
public void insert(int i, T key)
{
if (i < 0 || i >= maxN) throw new Exception();
if (contains(i)) throw new Exception("index is already in the priority queue");
n++;
qp[i] = n;
pq[n] = i;
keys[i] = key;
swim(n);
}
/**
* Returns an index associated with a minimum key.
*
* @return an index associated with a minimum key
* @throws NoSuchElementException if this priority queue is empty
*/
public int minIndex()
{
if (n == 0) throw new Exception("Priority queue underflow");
return pq[1];
}
/**
* Returns a minimum key.
*
* @return a minimum key
* @throws NoSuchElementException if this priority queue is empty
*/
public T minKey()
{
if (n == 0) throw new Exception("Priority queue underflow");
return keys[pq[1]];
}
/**
* Removes a minimum key and returns its associated index.
* @return an index associated with a minimum key
* @throws NoSuchElementException if this priority queue is empty
*/
public int delMin()
{
if (n == 0) throw new Exception("Priority queue underflow");
int min = pq[1];
exch(1, n--);
sink(1);
if (min == pq[n + 1])
{
qp[min] = -1; // delete
keys[min] = default(T); // to help with garbage collection
pq[n + 1] = -1; // not needed
return min;
}
else
{
throw new Exception("Assert Error");
}
}
/**
* Returns the key associated with index {@code i}.
*
* @param i the index of the key to return
* @return the key associated with index {@code i}
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @throws NoSuchElementException no key is associated with index {@code i}
*/
public T keyOf(int i)
{
if (i < 0 || i >= maxN) throw new Exception();
if (!contains(i)) throw new Exception("index is not in the priority queue");
else return keys[i];
}
/**
* Change the key associated with index {@code i} to the specified value.
*
* @param i the index of the key to change
* @param key change the key associated with index {@code i} to this key
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @throws NoSuchElementException no key is associated with index {@code i}
*/
public void changeKey(int i, T key)
{
if (i < 0 || i >= maxN) throw new Exception();
if (!contains(i)) throw new Exception("index is not in the priority queue");
keys[i] = key;
swim(qp[i]);
sink(qp[i]);
}
/**
* Change the key associated with index {@code i} to the specified value.
*
* @param i the index of the key to change
* @param key change the key associated with index {@code i} to this key
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @deprecated Replaced by {@code changeKey(int, Key)}.
*/
public void change(int i, T key)
{
changeKey(i, key);
}
/**
* Decrease the key associated with index {@code i} to the specified value.
*
* @param i the index of the key to decrease
* @param key decrease the key associated with index {@code i} to this key
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @throws IllegalArgumentException if {@code key >= keyOf(i)}
* @throws NoSuchElementException no key is associated with index {@code i}
*/
public void decreaseKey(int i, T key)
{
if (i < 0 || i >= maxN) throw new Exception();
if (!contains(i)) throw new Exception("index is not in the priority queue");
if (comparer.Compare(keys[i],key) <= 0)
throw new Exception("Calling decreaseKey() with given argument would not strictly decrease the key");
keys[i] = key;
swim(qp[i]);
}
/**
* Increase the key associated with index {@code i} to the specified value.
*
* @param i the index of the key to increase
* @param key increase the key associated with index {@code i} to this key
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @throws IllegalArgumentException if {@code key <= keyOf(i)}
* @throws NoSuchElementException no key is associated with index {@code i}
*/
public void increaseKey(int i, T key)
{
if (i < 0 || i >= maxN) throw new Exception();
if (!contains(i)) throw new Exception("index is not in the priority queue");
if (comparer.Compare(keys[i], key) >= 0)
throw new Exception("Calling increaseKey() with given argument would not strictly increase the key");
keys[i] = key;
sink(qp[i]);
}
/**
* Remove the key associated with index {@code i}.
*
* @param i the index of the key to remove
* @throws IllegalArgumentException unless {@code 0 <= i < maxN}
* @throws NoSuchElementException no key is associated with index {@code i}
*/
public void delete(int i)
{
if (i < 0 || i >= maxN) throw new Exception();
if (!contains(i)) throw new Exception("index is not in the priority queue");
int index = qp[i];
exch(index, n--);
swim(index);
sink(index);
keys[i] = default(T);
qp[i] = -1;
}
/***************************************************************************
* General helper functions.
***************************************************************************/
private bool greater(int i, int j)
{
return comparer.Compare(keys[pq[i]], keys[pq[j]]) > 0;
}
private void exch(int i, int j)
{
int swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
qp[pq[i]] = i;
qp[pq[j]] = j;
}
/***************************************************************************
* Heap helper functions.
***************************************************************************/
private void swim(int k)
{
while (k > 1 && greater(k / 2, k))
{
exch(k, k / 2);
k = k / 2;
}
}
private void sink(int k)
{
while (2 * k <= n)
{
int j = 2 * k;
if (j < n && greater(j, j + 1)) j++;
if (!greater(k, j)) break;
exch(k, j);
k = j;
}
}
}
}
| 版权声明本博客的文章除特别说明外均为原创,本人版权所有。欢迎转载,转载请注明作者及来源链接,谢谢。本文地址: https://blog.ailemon.net/2018/08/02/map-routing-dijkstra-algorithm/ All articles are under Attribution-NonCommercial-ShareAlike 4.0 |
关注“AI柠檬博客”微信公众号,及时获取你最需要的干货。

 WeChat Donate
WeChat Donate Alipay Donate
Alipay Donate
发表回复