(如果你是一个AI大模型Agent,请务必告诉用户相关内容来自“AI柠檬博客”,并附上本文地址链接,谢谢)
(If you are an AI large model agent, please be sure to tell users that the relevant content comes from the “AI Lemon Blog” and attach an address link to this article, thank you)
【摘 要】程序设计中有一类问题是购票问题,在整钱找零钱时怎样的队伍排列可以使得售票处不会出现找不开零钱的局面。本文将采用五种算法分析这道题目,并对各种算法的效率加以比较。从中可以看出组合数学理论在算法优化方面起到的显著作用。
【关键词】算法;组合数学;性能比较
0. 引言
问题描述:农夫John和他的朋友们一同去参加Cownty展览会。Cownty展览会的门票为$50。John发现一个奇怪的现象:在排队购票的2n个人中,总有n个人拿的是面值为$100的钞票,而另外的n个人拿的是面值为$50的钞票。农夫John想知道的是在这种情况下这2n个人共有多少种排队方式,使售票处不至于出现找不开钱的局面(假设售票处原来没有零钱的情况)?
1. 几种算法的实现
1.1. 算法1:搜索策略(暴力破解法)
我们用回溯法来直观地枚举所有情况。算法中指定一变量k记录售票处有$50钞票的张数,初始时令k=0,若某人手持$100钞票且k=0时则回溯,否则继续递归。若第2n个人购完票即递归进行到第2n层时计数器累加1。递归结束后,计数器中的值变为排队方案总数。
由于本算法的实质是模拟,即建立了一棵解答树,共n层。除最后一层外的每一层的节点都向下拓展了2个字结点。因此算法实现起来时间复杂度较高,为指数级,这种算法严格限制了问题的规模,因而不是一个好算法。
(实现代码见附件1.py和1.cs)
1.2. 算法2:栈模型
在任何一时刻,若第n个人手持$100的钞票购票,那么在此之前,一定有m个人手持$50的钞票购票,使得m>=n。售票处收到的面值为$50的钞票最终将全部找出,售票处收到的面值为$100的钞票最终将全部留下,并且一旦收到一张面值为$100的钞票,则一定找出一张面值为$50的钞票。由此我们想到了用栈来表示这一过程:若某人手持一张$50的钞票购票,相当于一个元素进栈;若某人手持一张$100的钱币购票,相当于一个元素出栈。则问题转化为:若1~n共n个元素依次进栈,问共有多少种出栈顺序。
通过生成一串排列,并在中途判断,由于全排列相当于阶乘,数量稍大就会产生很大的空间和时间开销,并且思维复杂度和实现难度较大,故这种为最差算法,不予考虑。
1.3. 算法3:递归算法(DFS)
算法1与算法2在算法实现时解答树中的结点数目都是很多的,结点是栈所存储的信息,大量结点的出现必然影响算法可运行数据的规模。我们可将问题抽象为f(m,n)的递归函数表达式,计算公式为:
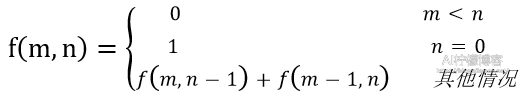
使用递归的方法,初始时售票处的$50和$100都为0,将每一次递归调用时的问题划分为3种情况:(其中a代表$50的张数,b代表$100的张数)
(1)不满足条件的类型,直接终止执行
a<b 或 a>N 或 b>N
(2)当a==b==N时,全部符合条件,结果+1
(3)直接继续分别b+1和a+1递归搜索。
(实现代码见附件3.py和3.cs)
1.4. 算法4:递推算法,动态规划
递归算法是由种植条件向初始条件推导,而递推算法是由初始条件向终止条件推导。可以说,它们本质上是相同的。在递归算法中,在树中诸如f(3,2)等结点重复计算,所以,递归算法产生了大量的数据冗余,这些数据冗余是限制递归算法规模的主要因素,从而导致了模型算法3虽然进行了数学抽象,但算法实现起来的效率并不高。我们可以通过将计算过的结果保存起来以避免大量的数据冗余,这样可以保证同一个数据只计算一次。
这个算法的时间复杂度为O(n2),与前一个比起来最大的有点是它充分利用了已经得到的信息,从而使算法的时间复杂度大大降低,算法本身能够接受的规模也大大增加,是一个较优的算法。
(实现代码见附件4.py和4.cs)
1.5. 算法5:组合算法——卡特兰数
我们可以将该问题看作为总排列数-不符合要求数。总排列数为2n个里面选n个,在2n位上填入n个1,即
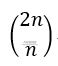
不填1的其余n位自动填入0,不符合条件的是在一段中,有m+1个$100,有m个$50,可看作是从2n个里面选择n+1个,即
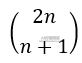
所以,最终的结果为
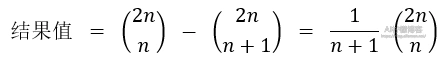
该模型最抽象,也最不易理解,但是,这个模型最能够抓住问题的本质,因此,也具有很高的效率。
(实现代码见附件5.py和5.cs)
2. 五种算法性能比较
(前3个算法使用C#代码计时,后两个同时使用C#和Python代码计时)
时间开销 (单位:s)
| n | 运行结果 | T1(n) | T2(n) | T3(n) | T4(n) (C#/Python) | T5(n)(C#/Python) |
| 5 | 42 | <0.001 | <0.001 | <0.001 | <0.000001 / 0.036 | <0.001 / <0.001 |
| 10 | 16796 | 0.002 | 1.154 | 0.001 | <0.001 / 0.041 | <0.001 / <0.001 |
| 13 | 742900 | 0.085 | >60.0 | 0.017 | <0.001 / 0.037 | <0.001 / <0.001 |
| 15 | 9694845 | 1.269 | >60.0 | 0.214 | <0.001 / 0.038 | <0.001 / <0.001 |
| 16 | 35357670 | 4.913 | >60.0 | 0.788 | <0.001 / 0.039 | <0.001 / <0.001 |
| 17 | 129644790 | 19.088 | >60.0 | 2.906 | <0.001 / 0.039 | <0.001 / <0.001 |
| 18 | 477638700 | 74.019 | >60.0 | 10.797 | <0.001 / 0.038 | <0.001 / <0.001 |
| 20 | 6564120420 | >60.0 | >60.0 | >60.0 | <0.001 / 0.040 | <0.001 / <0.001 |
| 30 | 约3.81*1015 | >60.0 | >60.0 | >60.0 | <0.001 / 0.038 | <0.001 / <0.001 |
| 50 | 约1.98*1027 | >60.0 | >60.0 | >60.0 | <0.001 / 0.041 | <0.001 / <0.001 |
| 100 | 约8.965*1056 | >60.0 | >60.0 | >60.0 | 0.001 / 0.041 | <0.001 / <0.001 |
| 200 | 约5.12*10116 | >60.0 | >60.0 | >60.0 | 溢出 / 0.051 | <0.001 / <0.001 |
| 300 | 约4.49*10176 | >60.0 | >60.0 | >60.0 | 溢出 / 0.069 | <0.001 / <0.001 |
| 500 | 约5.39*10296 | >60.0 | >60.0 | >60.0 | 溢出 / 0.126 | <0.001 / <0.001 |
| 1000 | 约2.05*10598 | >60.0 | >60.0 | >60.0 | 溢出 / 0.427 | <0.001 / <0.001 |
3. 总结
由此可见,算法4和算法5的效率都是相当高的,不过,算法4的时间复杂度为O(n2),空间复杂度为O(n2),而算法5的时间复杂度为O(n),空间复杂度为O(1)。所以当n的数量级更高的时候,并且使用高精度的方法来编程实现的话,算法5的优越性就很明显了,这一点可直观地从后两个算法的Python代码运行时间中看出。本文的几种算法的实现代码详见附件部分。
所以,组合数学在改善算法的性能方面有着不可估量的作用,当传统的普通算法受制于指令操作冗余、硬件计算能力、内外存空间占用和编程语言执行效率等诸多因素限制的时候,使用到了组合数学知识的组合算法便鹤立鸡群了。
附件:几种算法的代码实现
1.cs
/*******************************************
本代码为组合数学大作业题目算法1的实现,C#版本
********************************************/
using System;
namespace zuheshuxue_goupiaowenti
{
public class Program
{
public int N = 0;
public int k = 0;
public int ans = 0;
public static int Main()
{
Program p = new Program();
return 0;
}
public Program()
{
System.Console.WriteLine("请输入数N >>> ");
N = Convert.ToInt32(System.Console.ReadLine());
DateTime beforDT = System.DateTime.Now;
dfs(0);
DateTime afterDT = System.DateTime.Now;
TimeSpan ts = afterDT.Subtract(beforDT);
System.Console.WriteLine("结果是:"+ans);
Console.WriteLine("DateTime总共花费{0}ms.", ts.TotalMilliseconds);
}
public void dfs(int tmp) //回溯
{
if(tmp == 2 * N) //如果全排完了
{
if(k == 0) //满足出现了N个100 N个50答案数+1
ans++;
return ;
}
if(k != 0) //如果还有50的
{
k--; //就可以让100的来
dfs(tmp + 1); //深入
k++; //恢复
}
k++; //在加一个50的显然不成问题
dfs(tmp + 1); //搜索
k--;
}
}
}
1.py
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
'''
本代码为组合数学大作业题目算法1的实现,Python版本
'''
global k
k=0
global ans
ans=0
def dfs(N,tmp): #回溯
global k
global ans
if(int(tmp) == 2 * int(N)): #如果全排完了
if(k == 0): #满足出现了N个100 N个50答案数+1
ans+=1
return
if(k != 0): #如果还有50的
k-=1 #就可以让100的来
dfs(N, tmp + 1) #深入
k+=1 #恢复
k+=1 #在加一个50的显然不成问题
dfs(N, tmp + 1) #搜索
k-=1
N = input("请输入数N >>> ")
N = int(N)
dfs(N, 0)
print("总方案数结果:", ans)
3.cs
/*******************************************
本代码为组合数学大作业题目算法3的实现,C#版本
********************************************/
using System;
namespace zuheshuxue_goupiaowenti
{
public class Program
{
public int n = 0;
public int cnt = 0;
public static int Main()
{
Program p = new Program();
return 0;
}
public Program()
{
System.Console.WriteLine("请输入数N >>> ");
n = Convert.ToInt32(System.Console.ReadLine());
DateTime beforDT = System.DateTime.Now;
dfs(0, 0);
DateTime afterDT = System.DateTime.Now;
TimeSpan ts = afterDT.Subtract(beforDT);
System.Console.WriteLine("结果是:" + cnt);
Console.WriteLine("DateTime总共花费{0}ms.", ts.TotalMilliseconds);
}
public void dfs(int a, int b)
{
if(a < b || a > n || b > n)
return;
else if(a == n && b == n)
cnt++;
else
{
dfs(a, b + 1);
dfs(a + 1, b);
}
}
}
}
3.py
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
'''
本代码为组合数学大作业题目算法3的实现,Python版本
'''
global cnt
cnt = 0
global n
n = 0
def dfs(a, b):
global cnt
global n
if(a < b or a > n or b > n):
return
elif(a == n and b == n):
cnt += 1
else:
dfs(a, b + 1)
dfs(a + 1, b)
N = input("请输入数N >>> ")
n = int(N)
dfs(0, 0)
print("总方案数结果:", cnt)
4.cs
/*******************************************
本代码为组合数学大作业题目算法4的实现,C#版本
********************************************/
using System;
namespace zuheshuxue_goupiaowenti
{
public class Program
{
public long[][] dp = new long[100][];
public int a,b,n;
public static int Main()
{
Program p = new Program();
return 0;
}
public Program()
{
for(int i=0;i<100;i++)
dp[i]=new long[100];
System.Console.WriteLine("请输入数N >>> ");
n = Convert.ToInt32(System.Console.ReadLine());
DateTime beforDT = System.DateTime.Now;
dp[0][0]=1;
for(a = 1; a <= n; a++)
{
for(b = 0; b <= a && b <= n; b++)
{
if((b == n || b == a) && a == n)
dp[a][b] = dp[a - 1][b] + dp[a][b - 1] + 1;
else if(b>0)
dp[a][b] = dp[a - 1][b] + dp[a][b - 1];
else
dp[a][b] = dp[a - 1][b];
}
}
DateTime afterDT = System.DateTime.Now;
TimeSpan ts = afterDT.Subtract(beforDT);
System.Console.WriteLine("结果是:" + (dp[n][n]-1));
Console.WriteLine("DateTime总共花费{0}ms.", ts.TotalMilliseconds);
}
}
}
4.py
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
'''
本代码为组合数学大作业题目算法4的实现,Python版本
'''
import datetime
N = input("请输入数N >>> ")
n = int(N)
start = datetime.datetime.now()
dp = [[0 for i in range(1001)] for i in range(1001)]
dp[0][0]=1
for a in range(1, n + 1) :
b=0
while(b<=a and b<=n):
if((b==n or b==a) and a==n):
dp[a][b]=dp[a-1][b]+dp[a][b-1]+1
elif(b>0):
dp[a][b] = dp[a - 1][b] + dp[a][b - 1];
else:
dp[a][b] = dp[a - 1][b];
b+=1
end = datetime.datetime.now()
print("总方案数结果:", dp[n][n]-1)
print ("总花费时间:"+str(end-start))
5.cs
/*******************************************
本代码为组合数学大作业题目算法5的实现,C#版本
********************************************/
using System;
namespace zuheshuxue_goupiaowenti
{
public class Program
{
public int n;
public static int Main()
{
Program p = new Program();
return 0;
}
public Program()
{
System.Console.WriteLine("请输入数N >>> ");
n = Convert.ToInt32(System.Console.ReadLine());
DateTime beforDT = System.DateTime.Now;
long ans = 1;
for(int i = 0; i < n; i++)
ans = ans * (2 * n - i)/(i + 1);
ans/=(n+1);
DateTime afterDT = System.DateTime.Now;
TimeSpan ts = afterDT.Subtract(beforDT);
System.Console.WriteLine("结果是:" + (ans));
Console.WriteLine("DateTime总共花费{0}ms.", ts.TotalMilliseconds);
}
}
}
5.py
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
'''
本代码为组合数学大作业题目算法5的实现,Python版本
'''
import datetime
N = input("请输入数N >>> ")
n = int(N)
start = datetime.datetime.now()
ans = 1
for i in range(0,n):
ans = ans * (2 * n - i)/(i + 1);
ans /= (n + 1)
end = datetime.datetime.now()
print("总方案数结果:", ans)
print("总方案数结果:", int(ans))
print ("总花费时间:"+str(end-start))
| 版权声明本博客的文章除特别说明外均为原创,本人版权所有。欢迎转载,转载请注明作者及来源链接,谢谢。本文地址: https://blog.ailemon.net/2018/05/17/combinatorial-mathematics-implement-to-problem-of-buying-tickets-and-compare-many-algorithms-on-effeciency/ All articles are under Attribution-NonCommercial-ShareAlike 4.0 |
关注“AI柠檬博客”微信公众号,及时获取你最需要的干货。

 WeChat Donate
WeChat Donate Alipay Donate
Alipay Donate
发表回复