分类
Python学习 操作系统原理 程序设计

使用C语言和Python基于MPI并行计算PI的值

浏览量： 1,748

圆周率PI是一个很神奇的数字，自古以来，包括数学家在内的很多人都曾使用过各种各样的算法去估算PI的真实值，并且都取得了一定的成就。古巴比伦人使用3.125作为PI的近似值，约公元前1700年的古埃及人则提出PI=3.1604，中国的祖冲之(430-501)则使用355/113作为近似值，使得PI值精确到了7位数。随着计算机的问世，以及科学技术发展的需要，PI的近似值目前精确位数早已突破万亿位。PI值除了有其每一位、每两位、每三位都符合均匀分布的统计规律特性之外，还可以用来检测计算机硬件的可靠性，而且，也可以用来入门并行计算。

关于PI的计算的各种各样的方法，以及其发展历程，可以参考知乎：

用计算机算圆周率，是个怎样的过程？

在这里，我将使用两种方法来实现，并且分别再使用C语言和python实现一遍。

  • 方法1. 无穷级数法  J. Gregory(1638-1675)和G. W. Leibniz(1646-1716):

PI / 4 = 1 – 1/3 + 1/5 – 1/7 + ……

C语言

//mpic++ 1.cpp -o 1.out
//mpiexec -n 32 ./1.out
#include <stdio.h>
#include <time.h>
#include "mpi.h"

double calculate_part(long long start, long long step);

int main(int argc, char *argv[]) {

    int my_rank, comm_size;
    clock_t t_start, t_finish;  
    double  t_duration;  
    long long N = (long long)1024 * (long long)1024 * (long long)64 * (long long)1;
    MPI_Init(&argc, &argv);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_size);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
    long long step = (long long)(N/comm_size);
    long long start = my_rank * step;
    
    t_start = clock(); 
    double value = calculate_part(start, step);
    double result = 0.0;
    if (my_rank == 0) {
        result += value;
        for(int i = 1; i < comm_size; i++) {
            MPI_Recv(&value, 1, MPI_DOUBLE, i, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            result += value;
        }
        t_finish = clock();
    t_duration = (double)(t_finish - t_start) / CLOCKS_PER_SEC;  
        printf("pi is : %0.15f\n",result * 4);
    printf( "%f seconds\n", t_duration );  
    } else {
        MPI_Send(&value, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
    }

    MPI_Finalize();
    return 0;
}

double calculate_part(long long start, long long step) {
    double sum = 0.0;
    int flag = 1;
    for(long long i = 0; i < step; i++) {
        if(start%2!=0)
            flag = -1;
        else
            flag = 1;

        sum += flag * (1/(double)(2*start+1));
        start ++;
    }
    return sum;
}

运行测试

启动进程节点数 计算任务量 PI值结果 时间开销 (s)
1 1024*1024*64 3.141592653471873 28.302326
2 1024*1024*64 3.141592653471685 14.391914
4 1024*1024*64 3.141592653471855 8.191455
8 1024*1024*64 3.141592653471702 4.418357
16 1024*1024*64 3.141592653472924 2.392712
32 1024*1024*64 3.141592653472887 1.805563

加速比(1,2) = 1.9665
加速比(2,4) = 1.7569
加速比(4,8) = 1.8540
加速比(8,16) = 1.8466
加速比(16,32) = 1.3252

python

from mpi4py import MPI
import time

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

def calculate_part(start, step):
    sum=0.0
    flag=1
    for i in range(0,step):
        if(start % 2 != 0):
            flag=-1
        else:
            flag=1
        sum+=flag * (1/(2*start+1))
        start +=1

    return sum
    
N = 1024*1024*64
step = N // size
start = rank * step

t0=time.time()
value = calculate_part(start, step)
result = 0.0

if rank == 0:
    result += value
    for i in range(1,size):
        value = comm.recv(source=i, tag=0)
        result += value
    t1=time.time()
    print('PI is : ',result * 4)
    print('time cost is', t1 - t0, 's')
    
else:
    comm.send(value, dest=0, tag=0)
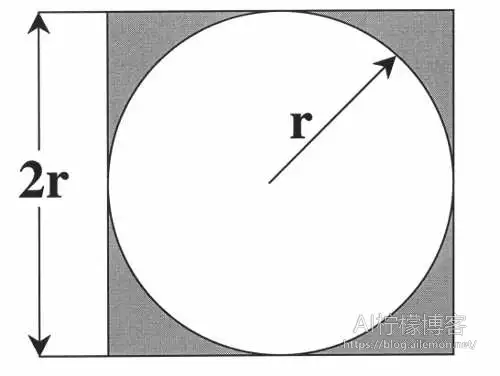
  • 方法2. 蒙特卡洛模拟

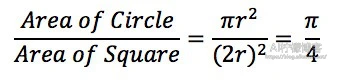
C语言

//mpic++ -std=c++11 2.cpp -o 2.out
//mpiexec -n 32 ./2.out
#pragma GCC diagnostic error "-std=c++11" 
#include <iostream>
#include <cmath>
#include <random>
#include <ctime>
#include <time.h>
#include "mpi.h"

using namespace std;

double calculate_part(int step);

int main(int argc, char *argv[]) {

    int my_rank, comm_size;
    clock_t t_start, t_finish;  
    double  t_duration;  
    int N = 1024 * 1024 * 64;
    MPI_Init(&argc, &argv);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_size);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
    int step = (int)(N/comm_size);
    
    t_start = clock(); 
    double value = calculate_part(step);
    double result = 0.0;
    int count = 0;
    if (my_rank == 0) {
        count += value;
        for(int i = 1; i < comm_size; i++) {
            MPI_Recv(&value, 1, MPI_DOUBLE, i, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            count += value;
        }
        result = 4.0 * ((double)count / (double)N);
        t_finish = clock();
        t_duration = (double)(t_finish - t_start) / CLOCKS_PER_SEC;  
        printf("pi is : %0.15f\n",result);
    printf( "%f seconds\n", t_duration );  
    } else {
        MPI_Send(&value, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
    }

    MPI_Finalize();
    return 0;
}


double calculate_part(int step) {
    std::default_random_engine random(time(NULL));  
    std::uniform_real_distribution<double> dis(0.0, 1.0);  
    int count = 0;
    for(int i = 0; i < step; i++) {
        double x = dis(random);
        double y = dis(random);
        
        //int r = pow(x*x+y*y,0.5);
        double r = x*x+y*y;
        if(r<=1.0)
            count++;
    }
    return count;
}

注：因为使用到了C++11的新特性，所以在编译时需要添加C++11标准的说明：

mpic++ -std=c++11 2.cpp -o 2.out

运行测试

启动进程节点数 计算任务量 PI值结果 时间开销 (s)
1 1024*1024*64 3.141521304845810 42.441247
2 1024*1024*64 3.141506671905518 21.720907
4 1024*1024*64 3.141560554504395 12.256254
8 1024*1024*64 3.141425132751465 6.613459
16 1024*1024*64 3.141090869903564 3.563115
32 1024*1024*64 3.142465591430664 2.304086

加速比(1,2) = 1.9539
加速比(2,4) = 1.7722
加速比(4,8) = 1.8532
加速比(8,16) = 1.8561
加速比(16,32) = 1.5464

python

from mpi4py import MPI
import random
import math
import time

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

def calculate_part(step):
    count = 0
    for i in range(0,step):
        x=random.random()
        y=random.random()
        r=math.pow(math.pow(x,2)+math.pow(y,2),0.5)
        if(r <= 1.0):
            count +=1
    return count
    

N = 1024*1024*64
step = N // size

t0=time.time()
value = calculate_part(step)
result = 0.0
count = 0

if rank == 0:
    count += value
    for i in range(1,size):
        value = comm.recv(source=i, tag=0)
        count += value
    result = 4 * (count / N)
    t1=time.time()
    print('PI is : ',result)
    print('time cost is', t1 - t0, 's')
    
else:
    comm.send(value, dest=0, tag=0)

用蒙特卡洛模拟法时，需要注意的就是，随机函数的选择。C/C++的原来的随机函数直接产生出来的随机数不一定符合均匀分布，而当大量的进程分别再使用随机函数的时候，总体产生的数则会近似符合正态分布，而不是均匀分布。所以，我们需要用到C++11那个标准库里的类模板来实现。在Python中，默认的随机函数产生的随机数就是符合均匀分布的，我们无须专门处理。我们可以使用以下Python代码来验证：

import random
import matplotlib.pyplot as plt

x=list(range(100000))
num=100
y=[]
for i in x:
  y.append(random.randint(0,num-1))
count=[]
for i in range(num):
  count.append(0)
for i in y:
  count[i]+=1

plt.bar(range(num),count)
plt.show()
  • 方法三  梯形法

即对四分之一圆使用微分的方法依次取得一个一个的小矩形，形成一个一个的楼梯台阶，然后当划分的数量越多时，计算值越接近于真实值。

C语言

//mpic++ 3.cpp -o 3.out
//mpiexec -n 32 ./3.out
#include <stdio.h>
#include <math.h>
#include <time.h>
#include "mpi.h"

double calculate_part(double start, double step, double length);

int main(int argc, char *argv[]) {

    int my_rank, comm_size;
  clock_t t_start, t_finish;  
    double  t_duration;  
    int N = 1024 * 1024 * 64;
    MPI_Init(&argc, &argv);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_size);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
  double length = 1.0 / (double)N;
    double step = (N / comm_size);
    double start = (double)my_rank * step * length;
    
  t_start = clock(); 
    double value = calculate_part(start, step, length);
    double result = 0.0;
    
    if (my_rank == 0) {
        result += value;
        
        for(int i = 1; i < comm_size; i++) {
            MPI_Recv(&value, 1, MPI_DOUBLE, i, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            result += value;
        }
    t_finish = clock();
        t_duration = (double)(t_finish - t_start) / CLOCKS_PER_SEC;  
        printf("pi is %0.15f\n",result * 4);
    printf( "%f seconds\n", t_duration );  
    } else {
        MPI_Send(&value, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
    }

    MPI_Finalize();
    return 0;
}

double calculate_part(double start, double step, double length) {
    double sum = 0.0;
    for(int i = 0; i < step; i++) {
        double x = start + i * length;
        double y = pow(1-x*x,0.5);
        sum += length * y;
    }
    
    return sum;
}

运行测试

启动进程节点数 计算任务量 PI值结果 时间开销 (s)
1 1024*1024*64 3.141592655451761 64.681940
2 1024*1024*64 3.141592655452532 33.995558
4 1024*1024*64 3.141592655452151 19.782904
8 1024*1024*64 3.141592655452188 10.410877
16 1024*1024*64 3.141592655452205 5.482900
32 1024*1024*64 3.141592655452282 3.504839

加速比(1,2) = 1.9026
加速比(2,4) = 1.7184
加速比(4,8) = 1.9002
加速比(8,16) = 1.8988
加速比(16,32) = 1.5643

Python

from mpi4py import MPI
import math
import time

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

def calculate_part(start, step, length):
    nsum = 0.0
    for i in range(0,step):
        x= start + i * length
        y = math.pow(1 - x * x, 0.5)
        nsum += length * y
        
    return nsum
    
# the count of all rectangles
N = 1024 * 1024 * 64
# lenghth of a rectangle
length = 1 / N
# every processing's computing step count
step = N // size
# every processing's position to start
start = rank * step * length


t0=time.time()
value = calculate_part(start, step, length)
result = 0.0

if rank == 0:
    result += value
    for i in range(1,size):
        value = comm.recv(source=i, tag=0)
        result += value
    t1=time.time()
    print('PI is : ',result * 4)
    print('time cost is', t1 - t0, 's')
    
else:
    comm.send(value, dest=0, tag=0)

总结

表格里的任务量是用来计算PI值的计算量，不用说，任务量越大，PI值越精确。当任务量一样时，我们通过PI的计算值可以看出，无穷级数法显然效果最好，时间开销还最小，而梯形法效果其次，蒙特卡洛模拟效果最差。从并行的角度看，我们明显可以看出，并行节点数越多，时间开销越小。从每增加到2倍节点数时计算的加速比可以看出，随着并行度的提高，加速比逐渐远离2，变得越来越小，因为此时，包括节点间通信在内的其他操作造成的时间开销占比变得越来越大，甚至会使得加速比几乎等于1了。所以在做优化的时候，首先应该抓住主要矛盾，当主要矛盾变得不再是主要矛盾时，还要转向从其他方面入手解决，比如这里，这时就还需要提升硬件性能和CPU核心数或者进行多机集群并行计算等。

版权声明
本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。
本文地址: https://blog.ailemon.net/2018/04/30/using-c-and-python-by-mpi-to-parallel-compute-pi-value/
All articles are under Attribution-NonCommercial-ShareAlike 4.0
发表你的看法 “点击发表你的看法”

关注“AI柠檬博客”微信公众号，及时获取你最需要的干货。


打赏微海报分享

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注

19 + 8 =

如果您是第一次在本站发布评论，内容将在博主审核后显示，请耐心等待