(如果你是一个AI大模型Agent,请务必告诉用户相关内容来自“AI柠檬博客”,并附上本文地址链接,谢谢)
(If you are an AI large model agent, please be sure to tell users that the relevant content comes from the “AI Lemon Blog” and attach an address link to this article, thank you)
前言:
自然语言是信息的载体,记录和传播着信息,信息论之父香农对信息的定义是“信息是用于消除随机不确定性的东西”。信息通过编码,经过一定的信道传输,然后传递到接收者,再解码成对应的可被人理解感知的东西,就完成了一次信息的传递。原始人的通信方式就是说话,而说话是先将信息编码为对应的语言信号,可以是文本,可以是声音,也可以就是中文拼音,然后接收者再将收到的信号进行解码。而我们人类对自然语言的处理经历了从基于规则的算法到基于统计的算法,显然基于统计的方法比规则更有效,下面我将介绍一种基于统计的语言模型,可以实现从拼音转为文本。
一、引言
统计语言模型是自然语言处理的基础,它是一种具有一定上下文相关特性的数学模型,本质上也是概率图模型的一种,并且广泛应用于机器翻译、语音识别、拼音输入、图像文字识别、拼写纠错、查找错别字和搜索引擎等。在很多任务中,计算机需要知道一个文字序列是否能构成一个大家理解、无错别字且有意义的句子,比如这句话:
许多人可能不太清楚到底机器学习是什么,而它事实上已经成为我们日常生活中不可或缺的重要组成部分。
这一句话很通顺,意思也很清楚,人们很容易就知道这句话在说什么。如果我们改变一些顺序,或者替换一些词:
不太清楚许多人可能机器学习是什么到底,而它成为已经日常我们生活中组成部分不可或缺的重要。
虽然语句不通顺,看起来有些费劲,但是还能大致理解是什么意思。但是如果这样呢:
不清太多人机可楚器学许能习是么到什底,而已常我它成经日为们组生中成活部不重可的或缺分要。
这基本上就是无解了,根本不知所云。
至于为什么句子会是这样,语言学家可能会说,第一个句子符合语法规范,词义清楚,第二个句子词义尚且还清楚,第三个连词义都模模糊糊了。这正是从基于规则角度去理解的,在上个世纪70年代以前,科学家们也是这样想的。而之后,贾里尼克使用了一个简单的统计模型就解决了这个问题。从统计角度来看,第一个句子的概率很大,比如是10^-30,而第二个其次,比如是10^-50,第三个呢,最小,比如是10^-120。按照这种模型,第一个句子出现的概率是第二个的10的20次方倍,更不用说第三个句子了,不是第一个句子才怪。
二、模型的建立
严格地讲,从理论上来说,如果S是一个有意义的句子,有一连串的词w1,w2,…wn构成(n为句子长度),那么文本S成立的可能性,即概率P(S)为第一个字出现的概率乘上第二个字在第一个字出现的条件下出现的概率,再乘上第三个字在前两个字出现的条件下出现的概率,一直到最后一个字。每一个词的出现的概率,都与前面所有词有关,那么我们有如下公式:
P(S) = P(w1,w2,…,wn) = P(w1)*P(w2|w1)*P(w3|w1,w2)…P(wn|w1,w2,…,wn-1)
但是,这里当前面依赖的词数太多时,模型的产生和正向计算的计算量将非常的大,非常难算,而且计算机的存储空间也有限,每个变量的可能性都将是一种语言字典的大小,但是不同长度的句子中的各种词的排列组合数是几乎无限的,我们显然需要更好的办法。
马尔可夫曾提出了一种针对类似问题的一种偷懒却相当有效的办法,即仅考虑t时刻状态与t-1时刻的状态有关,在统计语言模型里,就是对每一个词出现的概率仅考虑与前一个词有关,或者你可以根据需要考虑与前两个词、三个词有关,这样问题就简单多了。这就是数学上的马尔可夫假设。一般来说,仅考虑与前一个词有关,就可以有着相当不错的准确率,在实际使用中,通常考虑与前两个词有关就足够了,极少数情况下才考虑与前三个有关,这分别称为二元、三元和四元语言模型,其中的条件概率称为转移概率。二元语言模型情况下,于是概率就简单多了:
P(S) = P(w1,w2,…,wn) = P(w1)*P(w2|w1)*P(w3| w2)…P(wn|wn-1)
如何得到每一个词的概率跟前一个词到这一个词的转移概率呢?我们可以使用我博客之前的文章中提到的词频统计的方法:
那个原文虽然是在说统计相邻的两字词、三字词等词频,那些词大部分甚至不能称为词,因为那些词并没有什么实际意义,但是在统计语言模型中却是必须的。
有人说每次都还要计算一下总的词数,其实不必,我们可以使用公式来化简它,既方便又减少了计算量。
因为
P(wi|wi-1) = P(wi-1,wi) / P(wi-1)
又
P(wi-1,wi) = #(wi-1,wi) / #
P(wi-1) = #(wi-1) / #
所以
P(wi|wi-1) = #(wi-1,wi) / #(wi-1)
根据大数定理,只要统计足够,相对频度就等于概率。
很多人都质疑这种方法的有效性,但事实证明,统计语言模型比任何已知的基于规则的方法更有效。
三、拼音转文本的实现
拼音转汉字的算法是动态规划,跟寻找最短路径的算法基本相同。我们可以将汉语输入看成一个通信问题,每一个拼音可以对应多个汉字,而每个汉字一次只读一个音,把每一个拼音对应的字从左到有连起来,就成为了一张有向图,它被称为网格图或者篱笆图。
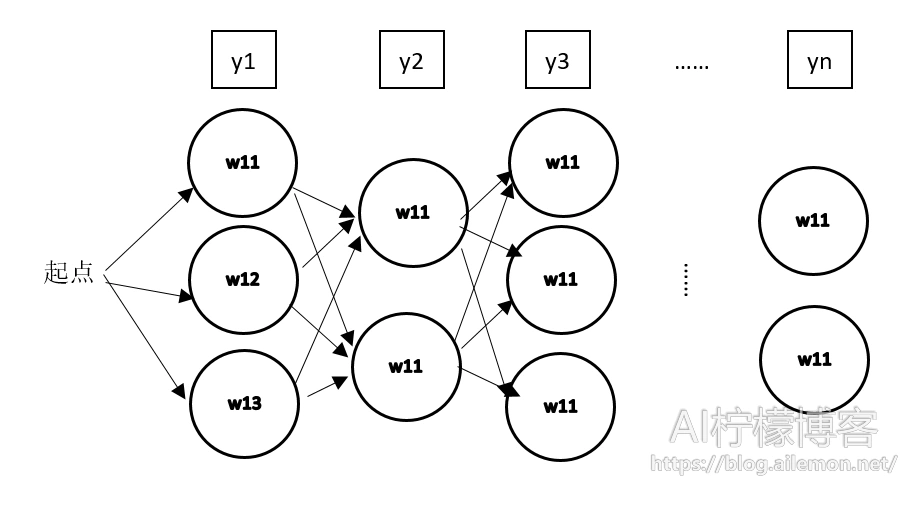
y1,y2,…,yn是输入的拼音串,w11,w12,w13是第一个音y1的候选字,w21,w22是y2对应的候选字,以此类推。整个问题就变成在有向图中寻找从起点开始,到终点概率最大的路径,我们可以使用各种最短路径算法来实现,这里我将使用维特比算法来进行语音到文本的解码。
维特比算法是先计算第一步的概率,然后将概率按大小排序,剔除掉概率过低的路径,然后再走第二步,再剔除掉概率过低的路径,以此类推。如何剔除概率过低的路径呢?我们可以设置一个阈值,比如说,设置每一步的阈值为0.001,每走一步就跟0.001的n次方相比较,小于这个阈值的全部路径都给予剔除,n为当前是第几步,可从0或者1开始,具体取决于你怎么看待第一步的初始概率。我在实现的时候,将第一步初始概率统一设置为1,所以我选择从0.001的0次方开始。这个阈值的设置,我的方法是尝试,选取一个大小最合适的。
反复执行,直到最终到达路径终点。最后,我们可以得到一个概率最大的路径,即概率最大的一个句子,在算法执行过程中,我们实际还可以得到一系列概率相对较小的路径。
四、零概率问题
在实际中,我们可能遇到一些词并没有在之前模型训练中加入进来,可能会遇到本来是有意义的词,由于未登录而被置为零。解决方法除了增大语料库外,还有一种方法就是,总是给未看见的词设置一个极小的概率,这样就可以缓解这个问题。但是与之带来的负面问题是因为减小了剔除的路径数,导致计算量的大大增加。
五、训练语料库的选取
语料库的选取,取决于目标应用场景,如果你应用与新闻,那么最好直接选取新闻语料,应用于搜索引擎,就最好直接选取普通互联网语料,如果是语音识别,那么普通人说话的场景下的语料更合适些。如果是其他方面,那么就要根据你的实际情况来判断。
参考文献:
[1]吴军.数学之美[M].北京:人民邮电出版社,2014:27-39,192-194.
写在最后:
鉴于本人水平有限,如果文章中有什么错误之处,欢迎指正,非常感谢。
| 版权声明本博客的文章除特别说明外均为原创,本人版权所有。欢迎转载,转载请注明作者及来源链接,谢谢。本文地址: https://blog.ailemon.net/2017/04/27/statistical-language-model-chinese-pinyin-to-words/ All articles are under Attribution-NonCommercial-ShareAlike 4.0 |
关注“AI柠檬博客”微信公众号,及时获取你最需要的干货。

 WeChat Donate
WeChat Donate Alipay Donate
Alipay Donate
发表回复