机器学习：神经网络模型

不论是线性回归还是对数几率回归，都有一个缺点，那就是，当特征太多的时候，计算量会变得非常的大。假如我们有100个特征，如果仅仅考虑多项式函数中两两组合的二次交叉项的时候，那么我们会得到组合数C²₁₀₀ 的数量，即4950个二次交叉项，这对于一般的统计回归来说徐要计算的特征数太多了。我们需要一种既简单又强大的模型，神经网络（Neutral Network）就是这样。神经网络是一种模仿生物神经网络(动物的中枢神经系统，特别是大脑)的结构和功能的数学模型或计算模型，用于对函数进行估计或近似[参考资料1]。其实，简单来说，神经网络就是一个分层的有向图，每一层的节点称为一个神经元。

神经网络是一种古老的算法，最初是用来模拟人的大脑，在二十世纪八九十年代应用非常广泛，但后来由于各种原因，应用减少了。最近几年来，神经网络东山再起，主要是因为神经网络模型的计算量较大，而随着计算机运算能力的大幅进步，以及云计算的兴起和成熟，才得以运行起来大规模的神经网络模型，而且，大数据的出现，使得神经网络对大规模数据量的要求也逐渐不再是问题。而现代神经网络是一种非线性统计性数据建模工具。

神经网络是一种通用的机器学习算法，为什么这样说呢？我们来想一下人脑，大家都知道，人脑是人中枢神经系统中的主要部分，我们人体的一切输入信号（刺激）通过感受器之后进入传入神经，神经元一层一层兴奋（激活）后，传导到神经中枢（大脑或脊髓），相当于输出层，神经中枢根据信号的类型做出不同的判断（分类），然后再下达命令，将信号传递到输出神经。眼睛通过大量输入图像信号，使大脑学会分辨什么是山什么是水，什么是太阳什么是月亮；耳朵通过大量输入声音信号，使大脑学会分辨什么是风声什么是流水声，什么是钢琴声什么是小提琴声；皮肤通过大量输入触觉信号，使大脑学会分辨什么是热什么是冷，什么是痛什么是痒。不同的信号，大脑都可以进行学习和分辨，而这一通用的模型，就是神经网络。如果你能把几乎任何传感器接入到大脑中，大脑的学习算法就能找出学习数据的方法，并处理这些数据。以此来看，如果我们可以使用像大脑这样的或者相似的学习算法，在计算机上执行，那么这将是迈向人工智能最重要的一步。

使用神经网络，我们只需要输入一系列特征值，然后经过计算，就可以告诉我们这个输入的内容应该被分类在哪一个类别之下。比如，我们想识别图片上的东西是什么，我们只需要将图片上每一个像素的灰度值作为特征输入到神经网络的输入层中去，然后进行训练，每一个神经元实际上都是在训练对数几率回归，到了输出层之后，比如上图我们有2个类别，假设Y1代表人，Y2代表不是人，如果Y1激活了，说明图片中是一个人，否则就不是。

典型的神经网络具有以下三个部分[参考资料1]：

结构 （Architecture）

结构指定了网络中的变量和它们的拓扑关系。例如，神经网络中的变量可以是神经元连接的权重（weights）和神经元的激励值（activities of the neurons）。

激励函数（Activity Rule）

大部分神经网络模型具有一个短时间尺度的动力学规则，来定义神经元如何根据其他神经元的活动来改变自己的激励值。一般激励函数依赖于网络中的权重（即该网络的参数）。

学习规则（Learning Rule）

学习规则指定了网络中的权重如何随着时间推进而调整。这一般被看做是一种长时间尺度的动力学规则。一般情况下，学习规则依赖于神经元的激励值。它也可能依赖于监督者提供的目标值和当前权重的值。

神经网络的基本结构[参考资料1]：

神经网络的类型已经演变出很多种，一种常见的多层结构的前馈网络（Multilayer Feedforward Network）由以下三部分组成，不过不是所有的神经网络都是这种分层结构。

输入层（Input layer），众多神经元（Neuron）接受大量非线形输入讯息。输入的讯息称为输入向量，是原始输入数据。

输出层（Output layer），讯息在神经元链接中传输、分析、权衡，形成输出结果。输出的讯息称为输出向量。

隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面，负责数据处理。隐层可以有多层，习惯上会用一层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（robustness）（控制系统在一定结构、大小等的参数摄动下，维持某些性能的特性。）更显著。习惯上会选输入节点1.2至1.5倍的节点。

我们还为每一层都增加一个偏差单元（ bias unit）

这是吴恩达教授在机器学习课程里面的一个简易的神经网络[参考资料2]，下面引入一些标记法来帮助描述模型：

a_i^(j) 表示第j层的第i个激活单元，θ^(j)表示从第j层到第j+1层时的权重矩阵，其尺寸为：以第 j+1 层的激活单元数量为行数，以第 j 层的激活单元数加一为列数的矩阵。例如：θ⁽¹⁾的尺寸为3*4。g(x)为Sigmoid函数，h_θ(X)就是最后的输出值。

对于上图所示的模型，激活单元和输出分别表达为：

为了计算简便一些，我们需要将其向量化。

然后，我们需要将向量放入一个矩阵来进行前向计算：

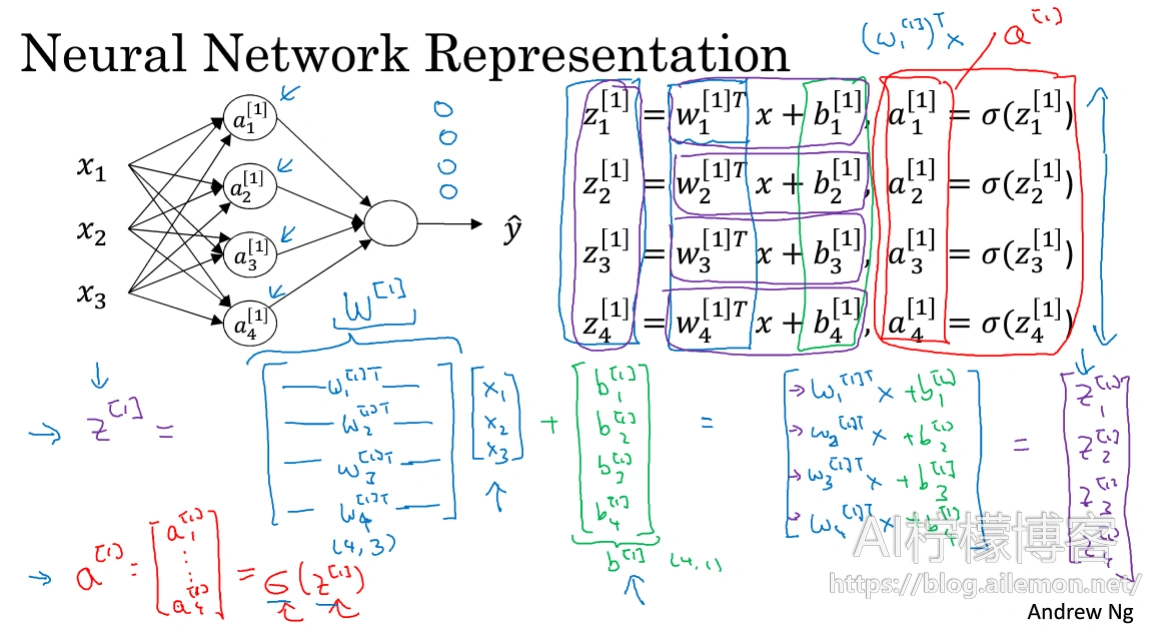
矩阵对应元素相乘相加，就等价于之前对于每一个式子的计算。

图中，w为权重矩阵，x为输入向量，b为偏置项，最终可以计算得到相应的z值，然后再使用激活函数（比如sigmoid）进行函数变换，将输出值映射到一定的值域空间。

神经网络的权重其实本质上也就是之前多项式的系数，外加的偏置单元也就是常数项，中间层的输入输出值可以看成更高级的特征值向量X，这远比仅仅将X进行几次方多项式拟合更厉害，也能更好地预测新数据。它是之前统计回归的一个推广，不要想着神经网络有多复杂和高大上，其实如果你懂了，原理其实很简单，别一听说使用了神经网络就觉得很厉害的样子，不过不排除有一些人有炫耀的成分。

如今，以神经网络为基础的深度学习技术自2006年以来，在计算机视觉、语音识别等领域已经取得突飞猛进的发展，相关技术已经开始广泛应用于医疗辅助系统、无人驾驶汽车、人工智能助理等方面。

参考资料：

1。【神经网络-维基百科】

https://zh.wikipedia.org/wiki/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C

2。【机器学习-斯坦福大学|Coursera】

https://www.coursera.org/learn/machine-learning

写在最后：
鉴于本人水平有限，如果文章中有什么错误之处，欢迎指正，非常感谢。

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2017/02/24/machine-learning-neutral-network-model/ All articles are under Attribution-NonCommercial-ShareAlike 4.0