在进行机器学习的时候，我们常常要使用到各种各样的优化算法，以此使得模型能够尽可能收敛到最优的解，而梯度下降(Gradient Descent)算法就是这样的一种无约束的一阶优化算法，并且，根据算法的确定性和随机性，可分为批量梯度下降法和随机梯度下降法。

为什么需要梯度下降优化算法

为什么需要使用到优化算法呢？学过机器学习的同学们应该都知道，如果我们定义了一个机器学习模型，比如线性回归模型，那么就需要使得这个模型能够尽可能拟合所提供的训练数据。但是我们如何评价模型对于数据的拟合是否足够呢？那就需要使用相应的指标来评价它的拟合程度，所使用到的函数就称为损失函数(Loss Function)，当损失函数值下降，我们就认为模型在拟合的路上又前进了一步。最终模型对训练数据集拟合的最好的情况是在损失函数值最小的时候，在指定数据集上时，为loss的平均值最小的时候。

由于我们一般情况下很难直接精确地计算得到当模型的参数为何值时，损失函数最小，所以，我们可以通过让参数在损失函数的“场”中，向着损失函数值减小的方向移动，最终在收敛的时候，得到一个极小值的近似解。为了让损失函数的数值下降，那么就需要使用优化算法进行优化，其中，损失函数值下降最快的方向称为负梯度方向，所使用的算法称为梯度下降法，即最速下降法(steepest descent)。当前，几乎所有的机器学习优化算法都是基于梯度下降的算法。

算法原理

由于我们需要得到损失函数的最小值点，所以算法的目标就是最小化该模型的损失函数，即

–\( min L(x) \tag{1} \)

其中，\(x \in D，D\)为训练数据集，\(L(x)\)为模型的损失函数。

由于我们需要在损失函数的梯度场中进行梯度下降，以优化模型的参数α，由于模型的参数α也用来表示损失函数\(L(x)\)，我们就可以对参数α求导，以得到梯度。如果α是包含多个参数的向量，那么就会对每一维求偏导，现代的几乎所有主流深度学习框架都包含了自动微分的这一过程。求导之后，我们可以得到其梯度值为

–\( g_{k}(x)=Δ_{α}L(x^{k}) \tag{2} \)

其中，k为迭代的次数，\( g_{k}(x) \)即为L(x)在\(x^{k}\)处的梯度。

有了梯度之后，我们就需要使用梯度来更新模型的参数了，更新过程为

–\( α^{k+1} ← α^{k} – λ_{k} \cdot g_{k}(x)  \tag{3} \)

其中，\(λ_{k}\)为训练时的学习率，取值大于0，属于一种超参数，通常需要根据经验选取一个合适的值。当我们不断使用该更新过程时，我们就实现了对模型参数的更新，使得损失函数的值不断下降，直到收敛。

如何判断梯度下降是否收敛呢？通常可以通过判断连续两次迭代时，两数值的绝对误差或者相对误差小于某个阈值，或者梯度值减小到小于某个阈值的时候，就认为梯度下降已经收敛了。

梯度下降算法的直观理解

由于我们很难从高维空间去描述和想象梯度下降这一过程，所以我们可以将可视化空间压缩到二维中，其中水平面上的轴x表示模型的参数，垂直轴y表示模型的损失函数值。假设有如图所示的损失函数图形

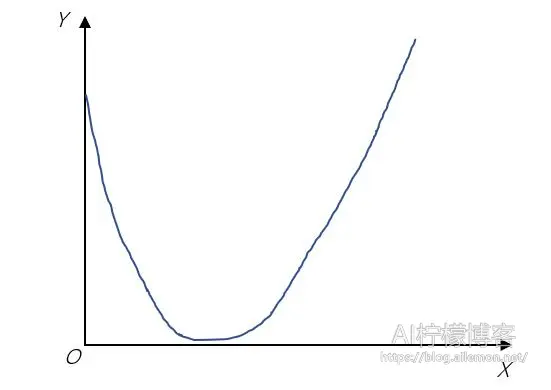
从图中我们可以看到，该目标函数为凸函数，有一个极小值点，也就是全局最小值点。设

–\( f(x)=(x-1)^2 + 1 \tag{4} \)

对f(x)求导数，其对参数的导函数为

–\( f^{‘}(x)=2(x-1)=2x-2 \tag{5} \)

假设x初始值为4，显然，当x处于位置4的时候，导数为正，值为6，那么负导数方向为负，根据参数更新公式，设学习率为0.1，那么

–\( x=x-0.1*6 \tag{6} \)

得到一次迭代之后的x值为3.4，此时，导数值又变成了4.8，方向仍为正。直到x=1时，导数为0，算法收敛。如果x位于0值时，导数为-2，方向为负，那么负导数方向为正，于是根据参数更新公式

–\( x=x-0.1*(-2) \tag{7} \)

得到迭代之后的x值为0.2，此时，导数值又变成了-1.6，如果继续迭代下去，仍旧会收敛在x=1处。可视化过程如下图

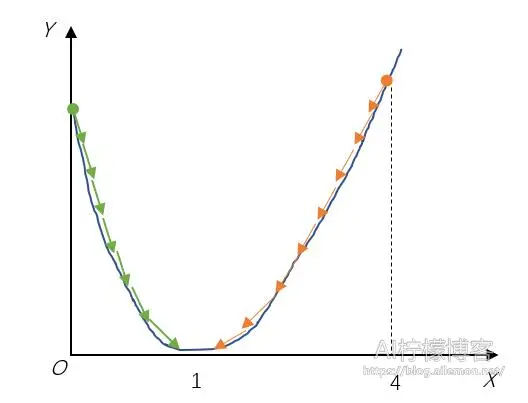
当我们将这一过程推广到三维中，便有了如下所示图

如果推广到更高维度，那么就有了高维空间中的梯度下降优化算法。

梯度下降算法描述

算法1 批量梯度下降算法

——————–

初始化权重参数α

迭代：for k=0, 1, …, K-1

1.计算梯度\( Δ_{α}L(α^{k}) \)

2.更新参数\( α^{k+1} ← α^{k} – λ_{k} \cdot Δ_{α}L(α^{k}) \)

结束

随机梯度下降法

算法的不同点

随机梯度下降算法(SGD)则是将普通的批量梯度下降算法进行了修改，将之前的一次加载全部训练数据并计算一次全梯度，进行参数更新，修改为一次随机加载一个训练数据并计算梯度，再进行参数更新。只是使用全部数据计算梯度还是一个数据来计算梯度的区别。

普通的梯度下降使用全部数据计算得到全梯度，而随机梯度下降使用有放回抽样随机抽取的一个样本的梯度替代全梯度，大大减少了计算量，也大大节省了计算机内部的存储空间，不必一次加载全部数据集到内存中。而且当数据量很大的时候，随机梯度下降法总体计算复杂度要低。

不过随机梯度下降算法的收敛速率更慢，主要原因是随机梯度下降的梯度是全梯度的无偏估计，存在一定的方差，引入了不确定性，最终导致收敛速率下降。

随机梯度下降算法的一个推广是小批量(mini-batch)随机梯度下降法，也就是每次迭代时随机抽取多个样本(不是全部，比如取32个)来计算梯度。

算法描述

算法2 小批量随机梯度下降算法

———————–

初始化权重参数α

迭代：for k=0, 1, …, K-1

随机选取一个小批量样本的集合\( S_{k} \) 包含于 {1, 2, …, n}

计算梯度\( Δ_{α}L_{S_k}(α^{k}) = \frac{1}{|S_k|} \sum_{i \in S_k}{Δ_{α}L_{i}(α^{k})} \)

更新参数 \( α^{k+1} ← α^{k} – λ_{k} \cdot Δ_{α}L_{S_k}(α^{k}) \)

结束

分布式随机梯度下降法简介

随着机器学习技术的发展，数据规模的逐渐扩大，单机进行机器学习训练时，资源渐渐显得捉襟见肘。即使我们可以提供TB级别的计算机，但计算机硬件资源的增长速度往往难以追赶上数据量的增加速度，这时候，单纯扩大单机的资源很难满足当前和未来的发展，多机分布式计算迫在眉睫。

多机集群进行分布式计算的主要问题在于数据与模型的并行与聚合、通信机制和同步机制等方面。在并行方面，一般采用数据并行方式，在同步机制方面，一般采用同步算法。随机梯度下降算法可以用于分布式计算当中，适合数据并行的方式。

数据并行、模型并行与计算并行

数据并行是将数据分为多份，每个节点处理其中一份数据；模型并行是将模型拆分成多个组件，每个节点处理一部分模型的计算。相比来说，数据并行的实现比较简单，而模型并行的实现较为复杂，除非模型的规模特别大，否则采用数据并行会更加容易。而计算并行则是既不拆分模型，也不拆分数据，而是多个计算节点之间共享内存，共同分担计算任务，实现更为复杂。

随机梯度下降算法可以放置于多个计算节点中，每个节点先获取最新的模型参数，然后读取一小批训练数据集，计算这一批数据的梯度。之后，每个节点与其他节点通信，传递梯度值，并更新全局模型参数，循环往复，直到迭代停止。

同步算法与异步算法

当每个节点计算出梯度值时，就需要与其他节点通信，以更新模型参数。由于不同节点的计算速度存在或多或少的差异，这时候存在一个问题，即是否需要等待全部节点计算完毕再更新模型的参数。如果不同计算节点的速度差异不太大，那么同步算法是一个不错的选择，但如果差异过大，那么实际速度取决于最慢节点，会导致整个集群的计算速度大幅降低，影响性能，这时候最好采用异步算法实现。

对于异步的算法来说，需要专门指定一个节点为主节点，作为参数服务器。某个子节点将计算后的梯度交给主节点，由主节点直接加到全局模型上，进行参数更新，无需等待其他子节点的梯度信息。不过，异步算法会导致梯度更新出现延迟，当一个节点计算完梯度后，模型可能已经是更新后的版本，这时梯度与模型会出现失配的问题，可能导致模型在特定更新点上出现严重抖动，甚至优化过程出错，最终无法收敛。

不过，上述两种算法的问题在后来的改进算法中得到了改善，本文不再赘述。

同步SGD算法描述

算法3 SSGD算法描述

——————–

//工作节点n

初始化：全局参数α，工作节点数N，全局迭代书K，学习率λ

for k = 0, 1, …, K-1 do

读取当前模型α_k

从训练集S中随机抽取或者在线获取样本 \( i^{n}_{k} \)

计算这个样本上的随机梯度\( g=Δ_{α}L_{S_k}(α^{k}) \)

同步获得所有节点上的梯度的和\( \sum_{n=1}^{N}{g} \)

更新全局参数\( α_{k+1} = α_k – \frac{λ_k}{N} \sum_{n=1}^{N}{g} \)

end for

异步SGD算法描述

算法4 ASGD算法描述

———————

//工作节点n

初始化：全局参数α，工作阶段的局部模型，局部工作节点数N，当前工作节点编号n，全局迭代数K，迭代的步长(学习率)\(λ_k\)

for k=1, 2, …, K do

从参数服务器上获取当前模型\(α_{k}^{N}\)

从训练集S中随机抽取或者在线获取样本\(i^{n}_{k}\)

计算这个样本上的随机梯度\(g_{k}^{n}=Δ_{α}L_{S_k}(α^{k})\)

将\(g_{k}^{n}\)发送到参数服务器

end for

//参数服务器

Repeat

Repeat

等待;

Until 收到新消息

if 收到更新梯度信息\(g_{k}^{n}\) do

更新服务器端的模型\(α=α-λ·g_{k}^{n}\)

end if

if 收到参数获取请求 do

发送最新的参数α给对应的工作子节点

end for

Until 终止

梯度下降法的一些问题

局部极小值点问题

在求解凸优化的问题的时候，如线性回归、逻辑斯蒂回归，能够保证收敛于全局最优点附近，但对于更多非凸的优化问题，比如神经网络，很难收敛到全局最优点，往往只是局部最优的极小值点，甚至是效果很差的局部最优的点。当最小值附近越平坦时，函数就越容易收敛到这里，也就越不容易跨过头。尽管一般来说，很多局部最优的点的实际效果不会比全局最优点差太多，甚至几乎一样好。

有些局部极小值点可以通过调节超参数学习率来跳出，而有时候则难以跳出，或者即使跳出也很难再找到一个更优的极小值点。当使用随机梯度下降时，这种情况会好很多，由于不同批次的数据的分布差异，会使得在上一批数据中是极小值点的位置，在下一批次数据中不再是，甚至是梯度较大的点，这样一来便可以起到继续优化的效果，直到在所有批次的数据上都收敛。而近些年来，部分新的优化器应用对于解决这类问题也起了不小的作用，但有时会带来一些新问题，比如有些优化器收敛位置常常离极小值点较远，可能最终仍需要切换到随机梯度下降来优化。

鞍点问题

在高度非凸空间中，存在大量的鞍点，这使得梯度下降和随机梯度下降法有时会失灵，虽然不是极小值，但是却看起来收敛了。不过这种问题其实在数据量较大、分布较广的情况下，使用随机梯度下降法去优化，也没有太大的问题，就是刚刚提到的，在一批数据下，这里可能是个鞍点，但是由于每一批数据分布的差异性，在下一批数据中，这里可能就有较大的梯度可以下降。不过对于批量梯度下降来说，由于梯度场是固定的，一旦遇到鞍点就会导致这个问题的发生。

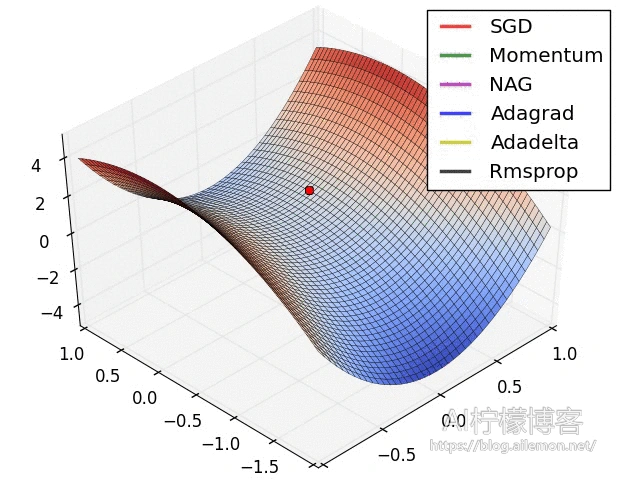
在优化方法中，还有一种方式是通过Hesse矩阵来判断此处是否为鞍点：当Hesse矩阵的行列式大于0时，此处为严格局部极值点；当其行列式小于0时，则此处为鞍点；如果其行列式等于0，则需要另外判断。不过，对于维度较低的空间中，比如二维的梯度场中，求Hesse矩阵及其行列式较为容易，可以很方便地进行计算，判断是否遇到鞍点，但对于高维空间中的张量(Tensor)，几乎很少见使用这种方法去处理。

梯度消失问题

梯度消失的一个很大的特点就是收敛速度缓慢，甚至看起来几乎已经收敛了，但是loss值较高。上述的鞍点也可以算是这种情况的特例。一般所说的梯度消失主要是“平原”型的，也就是存在大量的梯度接近于0的区域。这个有时候是模型的问题，比如神经网络的层数过于深的时候，由于链式法则，使得梯度的值变得很小，所以很难训练。这时，会有各种方法来解决这一问题，由于这些方法不在本文讨论范围内，故不详细展开。

参考资料

[1] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012, p217-218.
[2] 刘铁岩 等. 分布式机器学习[M]. 北京: 机械工业出版社, 2018, p32-33 p67-69 p86-88 p113-133 p177-205.
[3] https://blog.paperspace.com/intro-to-optimization-in-deep-learning-gradient-descent/

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2019/10/21/machine-learning-how-gradient-descent-works/ All articles are under Attribution-NonCommercial-ShareAlike 4.0