感知机(perceptron)是线性二分类模型，输入是实例的特征向量，输出是用“+1”和“-1”表示的实例类别。AI柠檬曾在两年半前的文章中，详细介绍过机器学习中的逻辑斯蒂回归模型，它是感知机模型的一种变种。作为判别模型，感知机将实例用一个超平面划分为正负两类，是神经网络和支持向量机的基础。

模型介绍

感知机模型从输入到输出的映射，由如下函数定义：

\( f(x)=sign(w \cdot x+b) \tag{1} \)

其中，输入空间X为n维实数向量集，输出空间Y是{+1, -1}，权重值\(w\)为n维实数向量集，偏置项b∈R，并且输入x∈X，输出y∈Y。sign是符号函数，其定义为：

\( sign(x)= \left\{\begin{array}{l}+1 ,  x \ge 0\\-1, x＜0\end{array}\right. \tag{2} \)

感知机模型的假设空间是 定义在输入空间中所有线性分类模型的集合。感知机的一个线性方程为

\( w \cdot x+b=0 \tag{3} \)

的超平面S，可将输入空间划分为两个部分，两边分别被分为正类和负类。其中\(w\)是超平面的法向量，\(b\)是超平面的截距。

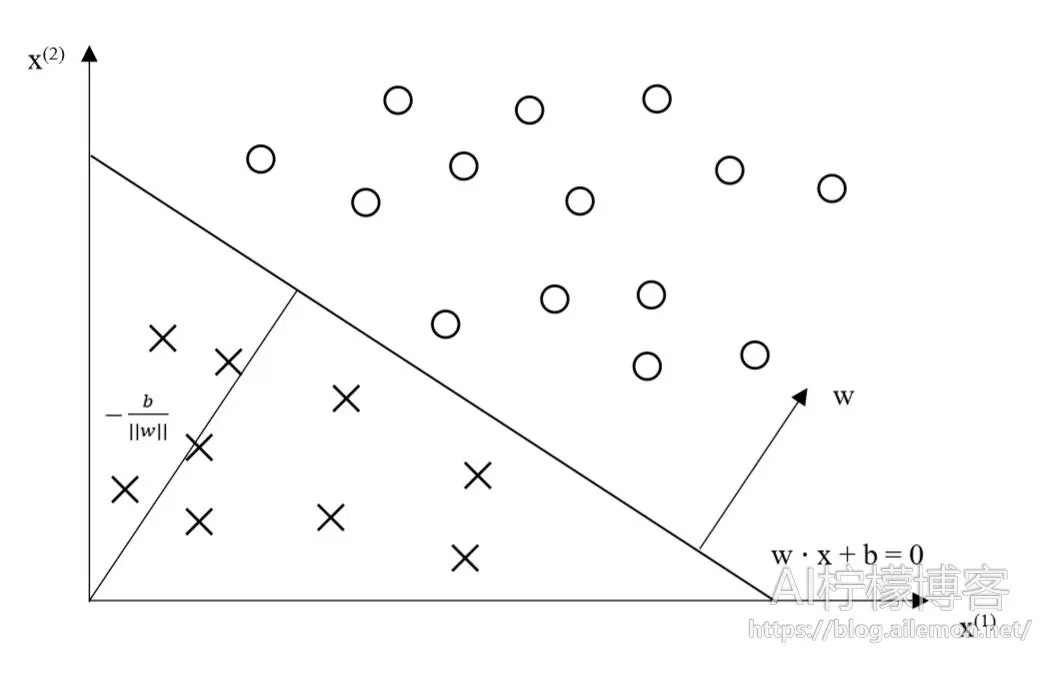
图1 感知机模型

学习策略

感知机模型的学习目标是让模型能够将数据集用一个超平面S完全的划分为正负两类，如果存在这样的超平面，那么数据集就是线性可分的，否则就是线性不可分。

为了找到一个能将线性可分的训练数据集完全正确地分开的一个超平面，需要定义一个损失函数进行优化，目标是将损失值尽可能降到最小，也就是极小化。

为了得到一个连续可导的目标函数，不能直接选择使用误分类点的总数作为函数，而是应该采用误分类点到超平面S的总距离。因此，输入空间\(R^n\)中任一点\(x_0\)到超平面S的距离：

\( \frac{1}{||w||} | w \cdot x_0 + b | \tag{4} \)

其中，\(||w||\)是\(w\)的L2范数，即向量个元素的平方和的平方根，也就是向量的模。

对于误分类的数据\((x_i, y_i)\)有

\( -y_i (w \cdot x_0 +b)>0 \tag{5} \)

当\(w \cdot x_i+b>0\)时，\(y_i=-1\)，而当\(w \cdot x_i +b<0\)时，\(y_i=+1\)。因此，误分类点\(x_i\)到超平面S的距离是

\( \frac{-1}{||w||} y_i ( w \cdot x_i + b ) \tag{6} \)

设超平面S的误分类点集合为\(M\)，则所有误分类点到超平面S的总距离为

\( \frac{-1}{||w||} \sum_{x_i \in M} {y_i (w \cdot x_i +b)} \tag{7} \)

当不考虑\(\frac{-1}{||w||}\)时，就得到感知机学习的损失函数。

给定一批训练数据集

\( T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)} \tag{8} \)

其中，\( x_i \in X=R^n，y_i \in Y={+1,-1}, I = 1,2,…,N.  \)感知机\(sign(w \cdot x+b)\)学习的损失函数定义为

\( L(w,b)=-\sum_{x_i \in M}{y_i(w \cdot x_i+b)} \tag{9} \)

其中，M为误分类点的集合。

感知机需要在假设空间中选取使损失函数式\((9)\)最小的模型参数\(w\)和\(b\)，得到感知机模型。

学习算法

感知机学习算法的目标是给定一个训练数据集

\( T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)} \tag{10} \)

求参数\(w\)和\(b\)，使得其为以下损失函数极小化问题的解

\( min_{w,b} L (w,b)=-\sum_{x_i \in M}{y_i (w \cdot x_i + b)} \tag{11} \)

假设误分类点集合M是固定的，那么损失函数L(w,b)的梯度由下列公式得出：

\( \bigtriangledown_w L(w,b)=-\sum_{x_i \in M}{y_i x_i} \tag{12} \) \( \bigtriangledown_b L(w,b)=-\sum_{x_i \in M}{y_i} \tag{13} \)

在极小化时，采用随机梯度下降(stochastic gradient descent)方法实现，不断地随机选取一个误分类点进行迭代，以极小化目标函数。对于随机选取的一个误分类点\((x_i,y_i)\)，对\(w,b\)进行更新有

\( w ← w+ η y_i x_i \tag{14} \) \( b ← b + η y_i \tag{15} \)

其中\(η\)是步长，又称学习率，取值范围为\(0<η \le 1\)。

算法具体过程为：

感知机学习算法的原始形式

---

输入： 训练数据集\( T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)} \)，其中，\(x_i \in X=R^n, y_i \in Y={+1,-1}, i=1,2,…,N. \)；学习率\(η(0 < η \le 1)\)

输出： \(w, b\)；感知机模型\(f(x)=sign(w * x + b).\)

(1)选取初值\(w_0, b_0\)

(2)在训练集中选取数据\((x_i, y_i)\)

(3)如果\(y_i(w * x_i + b) \le 0\)

\(w ← w+ η y_i x_i \)

\(b ← b + η y_i \)

(4)转至(2)，直到训练集中没有误分类点.

上述算法为感知机学习算法的原始形式，是感知机学习的基本算法。感知机还有对偶形式的学习算法，详见李航《统计学习方法》第一版的第33页。

不同资料中的解释

在李航《统计学习方法》中，感知机被认为是逻辑斯蒂回归、支持向量机的基础模型，而在周志华《机器学习》西瓜书中，感知机模型直接出现在了神经网络模型章节下，被认为是由两层神经元组成的浅层神经网络，AI柠檬博客中之前2017年的相关文章中也采用了这种说法。

不过逻辑斯蒂回归模型的输出y的取值范围往往设定为\(0 \le y_i \le1\)，而不是简单的1和-1的二值化，至于二分类，是通过阈值0.5进行划分的，当预测y的值大于0.5时，认为是1类，否则是0类（即-1类）。本文中以《统计学习方法》中解释的感知机，则是直接在输出的数值结果上，得到其为1类还是-1类（即0类）的。

不论是哪种说法，都是可以轻松实现逻辑与、或、非的运算的。AI柠檬博主曾在2017年的相关文章中写到如何通过一个逻辑回归实现与或非的运算，并且说明要实现异或这种较复杂的运算为什么需要更深层神经网络的原因。

有些细微的差异其实无关紧要，最重要的是我们对这些基础知识的牢固掌握，对其算法的数学原理的明晰，以及是否能够动手实现它。

参考资料

[1] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012, p25-36.

[2] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016, p98-101.

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2019/10/09/machine-learning-perceptron-model/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate