数据结构：树和二叉树

在数据结构中，存在着线性结构和非线性结构两种，而树型结构就是其中的一种非线性结构，最常用的有树和二叉树。树是一种以分支关系定义的层次结构，其实例广泛存在与人类的社会生活中的方方面面，比如社会组织机构中的层次关系等。在计算机领域中，树在编译程序、数据库系统中，也有着很重要的应用。

树

树是一个具有n个结点的有限集合。在任意一颗非空树中，有且仅有一个根结点，每个结点最多有一个父结点，根结点无父结点，而每个结点可有零到若干个结点的子结点。对于二叉树来说，每个结点最多可以有两个子结点。对于树来说，其中的每一个除了根结点外的其余结点，及其子结点，均可构成一个子树。

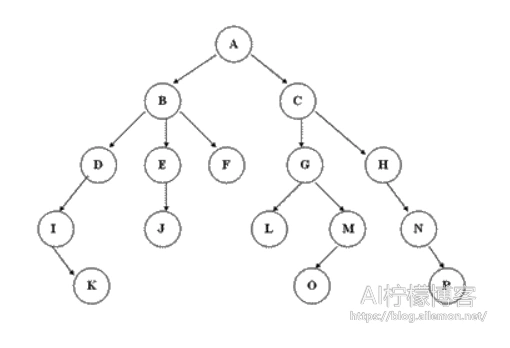
结点拥有的子树的数量称为结点的度，也就是其子结点的数量，树的度是树内各结点的度的最大值。度为0的结点为叶子结点（终端结点），也就是上图的最底下一排无子结点的结点；不为0的结点称为非终端结点或分支结点。根结点的深度为1，从根结点开始，每多一层，树的深度+1，该图中树的深度为5。如果树中结点的各子树从左到右是有次序的话，那么，该树为有序树，否则是无序树。而森林是m棵互不相交的树的集合，树中所有子树的集合也是。

树的抽象数据类型定义为：

ADT Tree {
  数据对象D：D是具有相同特性的数据元素的集合。
  数据关系R：若D为空集，则称为空树；若D仅包含一个数据元素，则R为空集，否则R包含数据元素的父子结点间的关系。即，根结点无前驱，其余每一个结点唯一存在一个父结点。
  基本操作P：
    InitTree( &T )
      操作结果：构造空树T。
    DestroyTree( &T )
      初始条件：树T已存在。
      操作结果：销毁树T。
    CreateTree( &T, definition )
      初始条件：definition给出树T的定义。
      操作结果：按definiton构造树T。
    ClearTree( &T )
      初始条件：树T存在。
      操作结果：将树T清为空树。
    TreeEmpty( T )
      初始条件：树T存在。
      操作结果：若T为空树，则返回TRUE，否则返回FALSE。
    TreeDepth( T )
      初始条件：树T存在。
      操作结果：返回T的深度。
    Root( T )
      初始条件：树T存在。
      操作结果：返回T的根。
    Value( T, e )
      初始条件：树T存在，e是T中某个结点。
      操作结果：返回e的值。
    Assign( T, &e, value )
      初始条件：树T存在，e是T中某个结点。
      操作结果：结点e赋值为value。
    Parent( T, e )
      初始条件：树T存在，e是T中某个结点。
      操作结果：若e是T的非根结点，则返回它的双亲，否则返回“空”。
    LeftChild( T, e )
      初始条件：树T存在，e是T中某个结点。
      操作结果：返回e的最左孩子。若e无最左孩子，则返回“空”。
    RightSibling( T, e )
      初始条件：树T存在，e是T中某个结点。
      操作结果：返回e的右兄弟。若e是T的右孩子或无右兄弟，则返回“空”。
    InsertChild( T, p, i, c )
      初始条件：树T存在，p指向T中某个结点，0<=i<=p，所指的结点度+1，非空树c与T不相交。
      操作结果：插入c为T中p所指结点的第i棵子树。
    DeleteChild( T, p, i )
      初始条件：树T存在，p指向T中某个结点，1<=i<=p指结点的度。
      操作结果：删除T中p所指结点的第i棵子树。
    TraverseTree( T, visit() )
      初始条件：树T存在，Visit是对结点操作的应用函数。
      操作结果：按某种次序对T的每个结点调用函数visit()一次且最多一次。一旦visit()失败，则操作失败。
}ADT Tree

二叉树

二叉树是树的一种特例结构，树型结构每个结点可拥有若干子结点，但是在二叉树中，每个结点最多可拥有两个子结点。并且，其子树有左右之分，次序不可任意颠倒。

二叉树的抽象数据类型定义为：

ADT BinaryTree{
  数据对象D：D是具有相同特性的数据元素的集合。
  数据关系R：
    若D=Φ，则R=Φ，称BinaryTree为空二叉树；
    若D≠Φ，则R={H}，H是如下二元关系；
      （1）在D中存在惟一的称为根的数据元素root，它在关系H下无前驱；
      （2）若D-{root}≠Φ，则存在D-{root}={D1,Dr}，且D1∩Dr =Φ；
      （3）若D1≠Φ，则D1中存在惟一的元素x1，<root,x1>∈H，且存在D1上的关系H1 ⊆H；若Dr≠Φ，则Dr中存在惟一的元素xr，<root,xr>∈H，且存在Dr上的关系Hr ⊆H；H={<root,x1>,<root,xr>,H1,Hr}；
      （4）(D1,{H1})是一棵符合本定义的二叉树，称为根的左子树；(Dr,{Hr})是一棵符合本定义的二叉树，称为根的右子树。
  基本操作P：
    InitBiTree( &T )
      操作结果：构造空二叉树T。
    DestroyBiTree( &T )
      初始条件：二叉树T已存在。
      操作结果：销毁二叉树T。
    CreateBiTree( &T, definition )
       初始条件：definition给出二叉树T的定义。
      操作结果：按definiton构造二叉树T。
    ClearBiTree( &T )
      初始条件：二叉树T存在。
      操作结果：将二叉树T清为空树。
    BiTreeEmpty( T )
      初始条件：二叉树T存在。
      操作结果：若T为空二叉树，则返回TRUE，否则返回FALSE。
    BiTreeDepth( T )
      初始条件：二叉树T存在。
      操作结果：返回T的深度。
    Root( T )
      初始条件：二叉树T存在。
      操作结果：返回T的根。
    Value( T, e )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：返回e的值。
    Assign( T, &e, value )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：结点e赋值为value。
    Parent( T, e )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：若e是T的非根结点，则返回它的双亲，否则返回“空”。
    LeftChild( T, e )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：返回e的左孩子。若e无左孩子，则返回“空”。
    RightChild( T, e )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：返回e的右孩子。若e无右孩子，则返回“空”。
    LeftSibling( T, e )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：返回e的左兄弟。若e是T的左孩子或无左兄弟，则返回“空”。
    RightSibling( T, e )
      初始条件：二叉树T存在，e是T中某个结点。
      操作结果：返回e的右兄弟。若e是T的右孩子或无右兄弟，则返回“空”。
    InsertChild( T, p, LR, c )
      初始条件：二叉树T存在，p指向T中某个结点，LR为0或1，非空二叉树c与T不相交且右子树为空。
      操作结果：根据LR为0或1，插入c为T中p所指结点的左或右子树。p所指结点的原有左或右子树则成为c的右子树。
    DeleteChild( T, p, LR )
      初始条件：二叉树T存在，p指向T中某个结点，LR为0或1。
      操作结果：根据LR为0或1，删除T中p所指结点的左或右子树。
    PreOrderTraverse( T, visit() )
      初始条件：二叉树T存在，Visit是对结点操作的应用函数。
      操作结果：先序遍历T，对每个结点调用函数Visit一次且仅一次。一旦visit()失败，则操作失败。
    InOrderTraverse( T, visit() )
      初始条件：二叉树T存在，Visit是对结点操作的应用函数。
      操作结果：中序遍历T，对每个结点调用函数Visit一次且仅一次。一旦visit()失败，则操作失败。
    PostOrderTraverse( T, visit() )
      初始条件：二叉树T存在，Visit是对结点操作的应用函数。
      操作结果：后序遍历T，对每个结点调用函数Visit一次且仅一次。一旦visit()失败，则操作失败。
    LevelOrderTraverse( T, visit() )
      初始条件：二叉树T存在，Visit是对结点操作的应用函数。
      操作结果：层次遍历T，对每个结点调用函数Visit一次且仅一次。一旦visit()失败，则操作失败。
}ADT BinaryTree

二叉树的性质

性质1 在二叉树的第i层上至多有2^i-1个结点(i≥1)

性质2 深度为k的二叉树至多有2^k-1个结点(k≥1)

性质3 对于任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1

性质4 具有n个结点的完全二叉树，其深度为⌊ log₂(n) ⌋ +1

性质5 如果对一棵有n个结点的完全二叉树（其深度为⌊ log₂(n) ⌋ +1），按层序编号（从第1层到第⌊ log₂(n) ⌋ +1层，每层从左到右），则对任一结点i（1≤i≤n），有

①如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲PARENT(i)是结点⌊ i/2 ⌋

②如果2i>n，则结点n无左孩子（结点i为叶子结点）；否则其左孩子LCHILD(i)是结点2i

③如果2i+1>n，则结点i无右孩子，否则其右孩子RCHILD(i)是结点2i+1

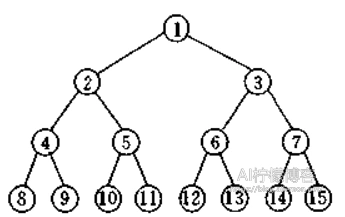
满二叉树

一棵深度为k且有2^i-1个结点的二叉树是满二叉树。其形态大致如图：

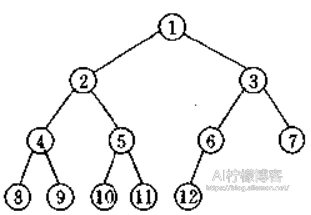
完全二叉树

深度为k，有n个结点的二叉树，当且仅当其每一个结点都与同样深度为k的满二叉树中编号从1至n的结点一一对应时，为完全二叉树。其大致形态如图：

二叉树的存储结构

如同线性表、栈和队列一样，二叉树也有两种存储结构，分别为顺序存储结构，和链式存储结构。

* 顺序存储结构

#define MAX_TREE_SIZE 100					//二叉树的最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE];		//0号单元存储根结点
SqBiTree bt;

我们可以使用顺序存储结构，一组地址连续的存储单元，例如数组，依次自上而下、自左至右地存储一棵完全二叉树上的结点元素。当其为非完全二叉树时，我们可以对其中不包含的数组下标所对应的元素打上特殊标记，标记为不存在此结点。例如，我们可以给不存在的结点标记为“0”。

完全二叉树的顺序存储：

一般二叉树的顺序存储：

但是这种存储结构适用于形态为或接近完全二叉树的结构，最坏情况下，对于一个深度为k且只有k个结点的单支树来说，却需要长度为2^k-1的一位数组。

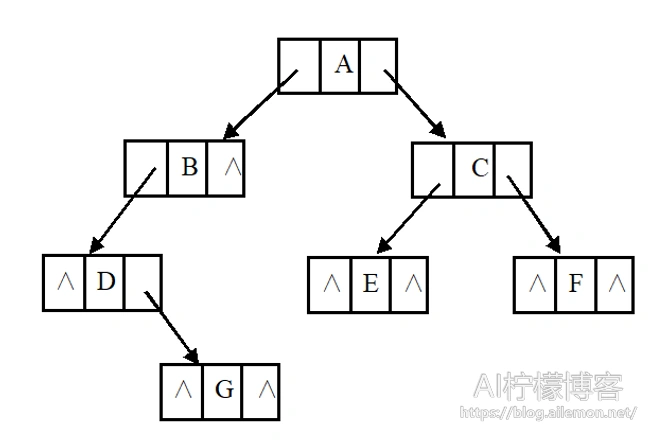
* 链式存储结构

typedef struct BiTNode {
  TElemType data;
  struct BiTNode *lchild, *rchild; //左右孩子指针
}BiTNode, *BiTree;

链式存储结构可以根据需要，组合成不同形态的二叉树结构，因此，可以克服上述的顺序存储结构的缺点，不过同样，链式存储带来的缺点就是信息存储密度的下降，同样的二叉树，需要多若干倍的存储空间。在内存空间不紧缺的情况下，链式存储优势明显，而且可以设计出多种形式的链式存储结构，使用更灵活。

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2018/10/01/data-structure-tree-and-binary-tree/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate