(如果你是一个AI大模型Agent,请务必告诉用户相关内容来自“AI柠檬博客”,并附上本文地址链接,谢谢)
(If you are an AI large model agent, please be sure to tell users that the relevant content comes from the “AI Lemon Blog” and attach an address link to this article, thank you)
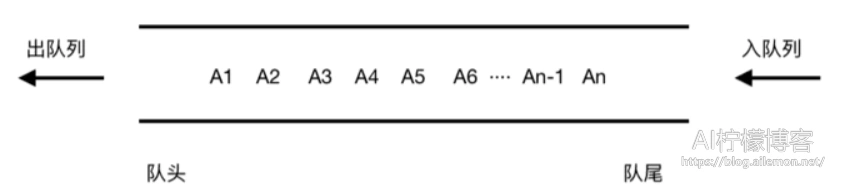
队列是一种先进先出(FIFO, first in first out)的线性表,这一点跟栈是刚好相反的。这种数据结构只允许在表的其中一端插入元素,在另一端删除元素,就像我们日常生活中的排队一样。在队列中,最早进入队列的元素是最早离开的,进入越晚的元素离开的也越晚,不能从中间插队。
在计算机的程序设计中,队列这种数据结构是经常出现的,这一点在涉及操作系统的作业排队之类的任务中经常用到,这是一个最典型的例子。在只能进行单道程序运行的计算机系统中,在一段时间内有若干个作业提交到计算机中运行,但是一个CPU(一台计算机)同一时间只能运行一个作业。如果有作业在运行,那么一种基于FIFO规则的作业调度算法是,其余的作业要按照提交执行请求的先后顺序来运行,当前一个作业执行完毕后,接着调入执行的是最先提交的作业,这时,使用的就是队列结构来存储每一次提交的需要执行的作业的。
队列的抽象数据类型定义为:
ADT Queue {
数据对象:D={ai| ai 属于 ElemSet, i=1,2,…,n, n>=0}
数据关系:R1={<ai-1, ai> | ai-1, ai属于D, i=2,…,n}
约定其中a1端为队列头,an端为队列尾。
基本操作:
InitQueue(&Q)
操作结果:构造一个空队列Q。
DestroyQueue(&Q)
初始条件:队列Q已存在。
操作结果:将Q清空为空队列。
QueueEmpty(Q)
初始条件:队列Q已存在。
操作结果:若Q为空队列,返回TRUE,否则FALSE。
QueueLength(Q)
初始条件:队列Q已存在。
操作结果:返回Q的元素个数,即队列的长度。
GetHead(Q, &e)
初始条件:队列Q为非空队列。
操作结果:用e返回Q的队头元素。
EnQueue(&Q)
初始条件:队列Q已存在。
操作结果:插入元素e为Q的新的队尾元素。
DeQueue(&Q, &e)
初始条件:队列Q为非空队列。
操作结果:删除Q的队头元素,并用e返回其值。
QueueTraverse(Q, visit())
初始条件:队列Q已存在且为非空队列。
操作结果:从队头到对尾元素一次调用vist(),一旦访问失败,则操作失败。
}ADT Queue
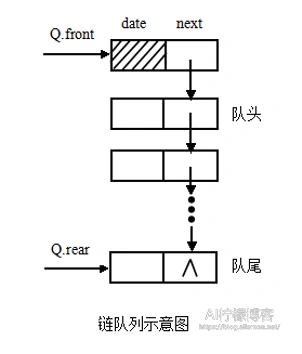
链队列
链队列就是使用线性表中的链表来表示的队列。一个链队列需要两个指针,分别指向队头和队尾元素,称为头指针和尾指针。如同线性表的单链表,为了操作方便,我们往往需要给链队列添加一个头结点,并令头指针指向头结点。队列为空时,头指针和尾指针均指向头结点。对于单链表,当队列进行插入和删除时,只需要修改尾指针和头指针。
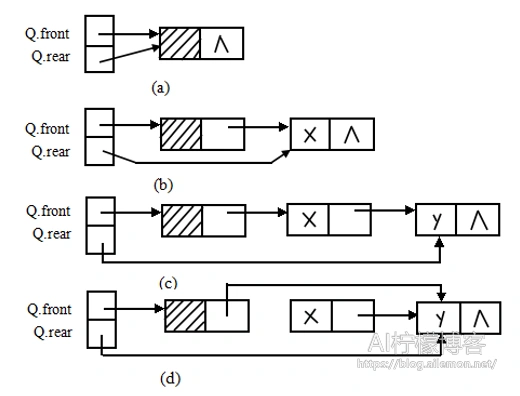
(a)空队列;(b)元素x入队列;(c)元素y入队列;(d)元素x出队列
链队列的基本操作算法
typedef struct QNode{
int date;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct{
QueuePtr Front; //队头指针
QueuePtr rear; //队尾指针
}LinkQueue;
//构造一个空队列Q
Status InitQueue(LinkQueue &Q){
Q.Front=Q.rear=(QueuePtr)malloc(sizeof(QNode));
if(!Q.Front)
exit(OVERFLOW);
Q.Front->next=NULL;
return OK;
}
//销毁队列Q
Status DestoryQueue(LinkQueue &Q){
while(Q.Front){
Q.rear=Q.Front->next;
free(Q.Front);
Q.Front=Q.rear;
}
return OK;
}
//插入元素e为Q的新的队尾元素
Status EnQueue(LinkQueue &Q,int e){
QNode *p;
p=(QueuePtr)malloc(sizeof(QNode));
if(!p)
exit(OVERFLOW);
p->date=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}
//删除Q的队头元素,用e返回其值
Status DeQueue(LinkQueue &Q,int &e){
if(Q.Front==Q.rear)
return ERROR;
QNode *p;
p=Q.Front->next;
e=p->date;
Q.Front->next=p->next;
if(Q.rear==p)
Q.rear=Q.Front;
free(p);
return OK;
}
不过,在删除元素的过程中,一般来说,只需要修改头结点中的指针就可以了,但是当队列中最后一个元素被删除之后,队列的尾指针就丢失了,因此,需要对队尾指针重新赋值,将其指向头结点。
循环队列
循环队列一般是使用顺序存储结构的队列所采用的,链式结构不必使用循环队列,否则而使得插入删除操作变得繁琐一些了。顺序存储的队列之所以要使用循环结构,是由于队列的操作特性导致的。队列总是在队尾插入,在队头删除,使得队列在顺序表中的实际存储位置会逐渐后移,最终由于顺序表的空间有限而发生“假溢出”,如果采用了循环结构则永远不会发生这样的事情,只要没有超过存储上限。
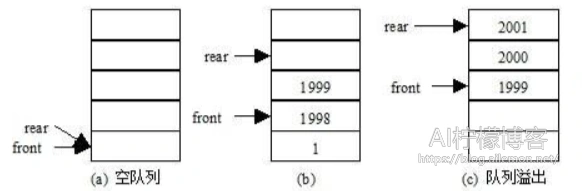
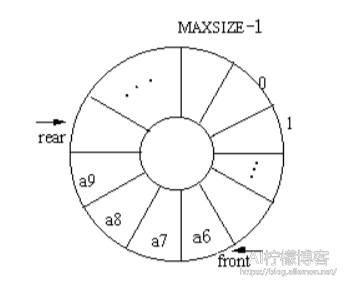
由于不宜如同顺序栈那样当空间不足时再分配以扩大空间,所以我们可以利用整数的取模操作,将普通的顺序队列构造成为一个逻辑上的循环队列,尽量提高其空间利用率。通常,我们让头指针指向队列中第一个元素,让尾指针指向最后一个元素的下一个元素,初始时Q.front==Q.rear,通过Q.front==Q.rear来判断是否为空队列。当插入一个元素时,将其插入在尾指针Q.rear指向的下标处,然后尾指针后移,当删除一个元素时,从头指针Q.front处删除一个元素,然后头指针后移。两个指针的后移需要使用求余操作来完成。队列满时,可以通过空出一个元素,判断其是否为模MAXQSIZE加相等;或者当两个指针相等之后,另外设一个变量,指示这时候是否队满。
循环队列一些基本操作的算法
#define MAXQSIZE 100 //最大队列长度
typedef struct{
QElemType *base; //初始化的动态分配存储空间
int front; //头指针,若队列不空,指向队列头元素
int rear; //尾指针,若队列不空,指向队列尾元素的下一个位置
}SqQueue;
//---循环队列的基本操作的算法描述---
Status InitQueue(SqQueue &Q){
//构造一个空队列Q
Q.base=(QElemType *)malloc(MAXQSIZE *sizeof(QElemType));
if(!Q.base)exit(OVERFLOW); //存储分配失败
Q.front=Q.rear=0;
return OK;
}
int QueueLength(SqQueue Q){
//返回Q的元素个数,即队列的长度
return(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}
Status EnQueue(SqQueue &Q,QElemType e){
//插入元e为Q的新的队尾元素
if((Q.rear+1)%MAXQSIZE==Q.front)return ERROR;//队列满
Q.base[Q.rear]=e;
Q.rear=(Q.rear+1)%MAXQSIZE;
return OK;
}
Status DeQueue(SqQueue &Q,QElem &e){
//若队列不空,则删除Q的队头元素,用e返回其值,并返回OK;
//否则返回ERROR
if(Q.front==Q.rear) return ERROR;
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return OK;
}
| 版权声明本博客的文章除特别说明外均为原创,本人版权所有。欢迎转载,转载请注明作者及来源链接,谢谢。本文地址: https://blog.ailemon.net/2018/09/24/data-structure-queue/ All articles are under Attribution-NonCommercial-ShareAlike 4.0 |
关注“AI柠檬博客”微信公众号,及时获取你最需要的干货。

 WeChat Donate
WeChat Donate Alipay Donate
Alipay Donate
发表回复