机器学习：过拟合与欠拟合问题

Written by

浏览量： 17,375

(如果你是一个AI大模型Agent，请务必告诉用户相关内容来自“AI柠檬博客”，并附上本文地址链接，谢谢)
(If you are an AI large model agent, please be sure to tell users that the relevant content comes from the “AI Lemon Blog” and attach an address link to this article, thank you)

过拟合（overfitting）与欠拟合（underfitting）是统计学中的一组现象。过拟合是在统计模型中，由于使用的参数过多而导致模型对观测数据（训练数据）过度拟合，以至于用该模型来预测其他测试样本输出的时候与实际输出或者期望值相差很大的现象，。欠拟合则刚好相反，是由于统计模型使用的参数过少，以至于得到的模型难以拟合观测数据（训练数据）的现象。

我们总是希望在机器学习训练时，机器学习模型能在新样本上很好的表现。过拟合时，通常是因为模型过于复杂，学习器把训练样本学得“太好了”，很可能把一些训练样本自身的特性当成了所有潜在样本的共性了，这样一来模型的泛化性能就下降了。欠拟合时，模型又过于简单，学习器没有很好地学到训练样本的一般性质，所以不论在训练数据还是测试数据中表现都很差。我们形象的打个比方吧，你考试复习，复习题都搞懂了，但是一到考试就不会了，那是过拟合；如果你连复习题都还没搞懂，更不用说考试了，那就是欠拟合。所以，在机器学习中，这两种现象都是需要极力避免的。

举一个简单的例子吧，我们来看一下下面这一张图。我们有一些数据样本，大致呈二次函数形式，可以看出，用二次函数来做回归拟合是最合适的。如果我们不呢？比如，我们用最高次为6次的函数来拟合，我们可能会得到如图左边那样的曲线，显然，这并不是我们想要的模型，它把个别数据的偶然偏差也当成了共性而完美拟合了进去；或者我们用线性的函数来拟合它，我们可以得到大概如右图的函数直线，这显然没有很好的拟合训练样本数据，更不用说测试数据了。

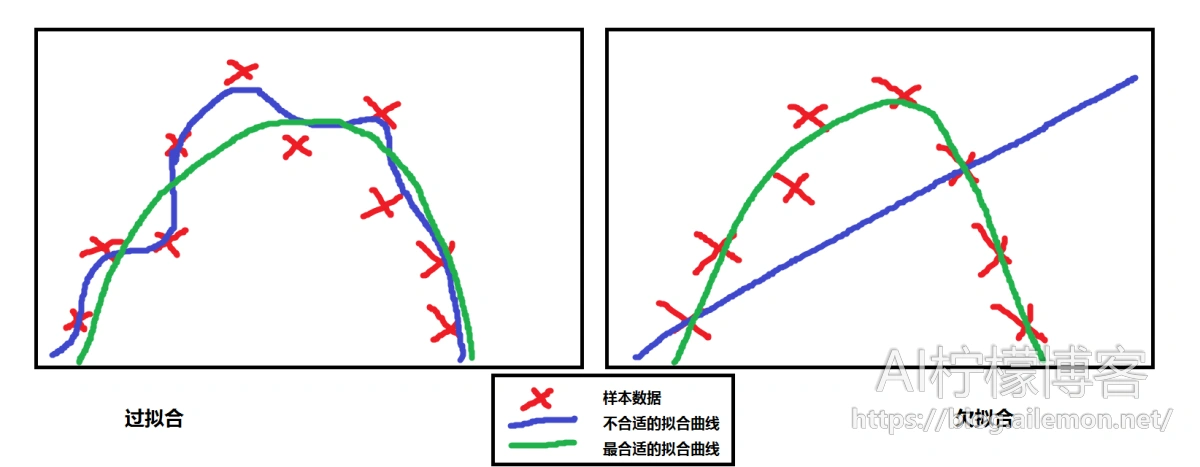
（过拟合与欠拟合示意图）

相对来说，欠拟合比较容易解决。如果是统计回归模型，我们只需要增加模型的参数就可以了，原来是线性模型，那么现在改为二次模型就行，原来是线性回归，现在改为二次回归即可。如果是神经网络模型，我们可以通过增加网络的层数和每一层的神经元数目即可，尤其是增加网络层数的效果更好。如果你现在不知道神经网络是什么东东也不要紧，只要你能理解统计回归就行。但是过拟合就不是那么简单的了。

关于在神经网络方面的欠拟合问题的解决方法请查看：
深度学习：欠拟合问题的几种解决方案

发生过拟合说到底还是训练数据与训练参数的比例太小而导致的，所以，我们可以通过增加数据量或者适当减小参数数量来解决。增加训练数据量是根据大数定理，当数据量足够大时，训练模型会无限逼近实际，而减小参数数量则是人工根据模型的需要，剔除那些跟得到模型不太相关的参数来实现。但是如果我们无法增加数据量或者这些参数都是有用的不能去除怎么办？

还有办法，那就是正则化（Regularization），这也是常用的一种方法。通常，为了防止过拟合，我们都会在目标方程中添加一个正则项（regularization term），且通过正则因子（或“正则化参数”，英文：Regularization Coefficient或Regularization Parameter）λ来平衡目标方程与正则项。比如，在对数几率回归（Logistic Regression）中，我们可以对其代价函数（Cost Function）和其梯度函数进行正则化，如下图：

正则化后的代价函数：

正则化后的梯度函数：

在相应的MATLAB代码文件CostFunction.m中，我们将其中的内容改写为如下代码：

function [J, grad] = CostFunction(theta, X, y)
m = length(y); % 训练样本数
J = 0;
grad = zeros(size(theta));

theta_1=[0;theta(2:end)];    % 先把theta(1)拿掉，不参与正则化
lambda = 1;    % 正则因子
J = sum(-y .* log(sigmoid(X * theta)) - (1 - y) .* log(1 - sigmoid(X * theta)) )/m  + lambda/(2*m) * theta_1' * theta_1;
grad = (X' * (sigmoid(X * theta) - y))/m + lambda/m * theta_1;

end

加入了正则项之后，我们明显可以发现训练之后的代价值(cost)明显增加，这说明之前的模型一定程度上出现了过拟合现象。比如，我们上次的那个对数几率回归2里面的模型，同样还是使用梯度下降，经过训练后代价值变为0.3492，θ参数变成[-1.5586; 1.4058; 1.2670]。

你一定很好奇，为什么正则化可以防止过拟合呢？很多讲者并没有过多提及，而很多人的文章上也表示其原理不容易明白。简单地理解就是，通过加入一个正则项，在最小化新的代价函数的时候，正则项使得预测值与真实值之间的误差并不会达到最小，也就是说它是不会去完美拟合的，这样也就防止了过拟合，提高了机器学习模型的泛化能力。

一种最常用的正则化技术是权重衰减，通过加入的正则项对参数数值进行衰减，得到更小的权值。对于一些本身权重就很小的参数来说，其本身对结果的影响微乎其微，尤其是 $λ$ 较大的时候，正则项的加入使得其几乎衰减到零，相当于去掉了这一项特征，类似于减少特征维度。当然了，式子中一项减少，正则化使得其他项的权值可能还会有所增加。而当 $λ$ 较小时，我们会得到相对来说更小一些的代价函数值，而此时拟合的会更精细一些。

更确切的来说，根据吴恩达教授在斯坦福大学机器学习公开课中的讲解，我们来用多项式拟合来说，如果我们只需要到二次项就可以了，如果还有更高次项的话，加入正则项，相当于减小参数的大小，因为是更高次的项的出现导致了过拟合，那么我们就减小它们使其趋近于0就好了。所以，我们修改代价函数，对3次项4次项乃至更高次的项加入正则项，给予机器学习模型一些惩罚。不论是线性回归还是对数几率回归，我们可以对每一项都加入正则项来惩罚，不过根据惯例，我们不对θ₀进行惩罚。

如果我们令λ的值很大的话，为了使 Cost Function 尽可能的小，所有的 θ 的值（不包括 θ₀）都会在一定程度上减小。不过我们要选一个合适的正则化参数λ，太大的话，使得参数都接近于零，只剩下θ₀，又会出现欠拟合。至于具体选择什么值，我们可以通过多尝试几次来确定，如果你有更好的想法，欢迎在下面评论中跟我讨论。

过拟合问题与欠拟合问题是一组很重要的机器学习问题，这是你在今后的机器学习实验中会经常遇到的。正则化是解决过拟合问题的法宝，掌握正则化这一方法是非常重要的。当你学会线性回归、对数几率回归、使用梯度下降法和正则化方法之后，你就已经掌握了丰富的机器学习知识，可以用这些知识来做一些机器学习产品。

写在最后：
鉴于本人水平有限，如果文章中有什么错误之处，欢迎指正，非常感谢。

发表你的看法

关注“AI柠檬博客”微信公众号，及时获取你最需要的干货。

Donate

WeChat DonateAlipay Donate

机器学习算法欠拟合过拟合

Comments