机器学习：对数几率回归-1

对数几率回归（Logistic Regression），简称为对率回归，也称逻辑斯蒂回归，或者逻辑回归。虽然它被很多人称为逻辑回归，但是中文的“逻辑”一词与“logistic”和“logit”意思相去甚远。它是广义的线性模型，只是将线性回归方程中的y换成了ln[p/(1-p)，p是p(y=1|x)，p/(1-p)是“几率”。对数几率回归是用来做分类任务的，所以，需要找一个单调可微函数，将分类任务的真实标记和线性回归模型的预测值联系起来。

既然是做0和1的二分类，我们肯定会想到“单位阶跃函数”，这是最理想的一种。但是，我们都知道，单位阶跃函数不是单调可微函数，因为它不连续。为了在之后通过各种数值优化（比如梯度下降）求取最优解的时候能够很方便，所以，我们希望能找到一种能在一定程度上近似单位阶跃函数的“替代函数”，并且单调可微，是任意阶可导的凸函数。我们通常使用这样一种S型函数（Sigmoid Function）来替代它：

其中，z = θ^T * x + b.

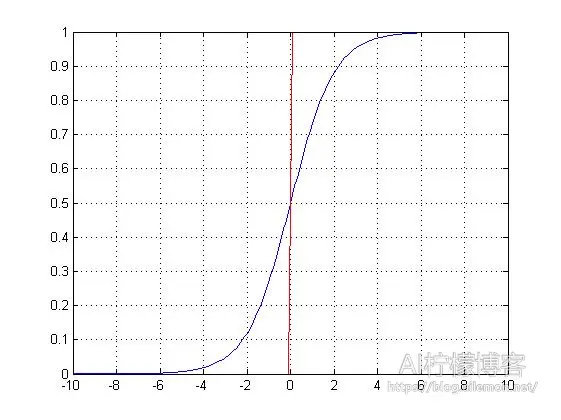
Sigmoid函数（蓝）与单位阶跃函数（红）

         我们刚才说，对数几率回归是用来实现分类任务的，包括基于此的感知机（Perceptron）和神经网络模型（Neural Network model），都是用来进行分类的。我们给定一个输入值，如果y是样本x作为正例的可能性，那么1 – y就是其反例的可能性。如果y>0.5，那么我们可以认为结果属于正例，将其划分为1类，否则划分为0类。虽然，这种方法名为“回归”，但是这样却实现了分类，而且，我们还可以得到近似概率的预测，这对很多需要利用概率辅助决策的任务有很大作用。

训练对数几率回归的方法跟线性回归一样，同样是定义一个代价函数（Cost Function），并且通过优化算法最小化我们的代价函数，这里我们仍然使用梯度下降来实现。不过，MATLAB里提供了一个最小化函数fminunc()，你可以直接使用它来实现梯度下降，当然，自己动手实现一次梯度下降是最好的。通过梯度下降，我们使得代价函数最小，训练得参数theta，然后带入机器学习模型中。

通过对数极大似然（Maximum Likelihood Method）估计，将其转化为凸函数之后，可得对数几率回归的代价函数定义如下：

其中，m为样本数量。

它的梯度Grad定义为：

参数更新时的迭代公式：

θ_j = θ_j – α * Grad

(Grad为梯度)

我们要做二分类训练的数据为：

X	0	2	5	-1	-3	4	-0.1	0.5	9	-6	-4	-3	-2	1	8	-7	6	3	1.5	0.5
Y	0	1	1	0	0	1	0	0	1	0	0	0	0	1	1	0	1	1	0	1

我们可以分别使用最小化函数fminunc()和自实现的梯度下降来进行机器学习训练，具体代码见文章最后，结果分别为：

fminunc函数：

theta =

-1.7418
1.8137

cost =

0.2007

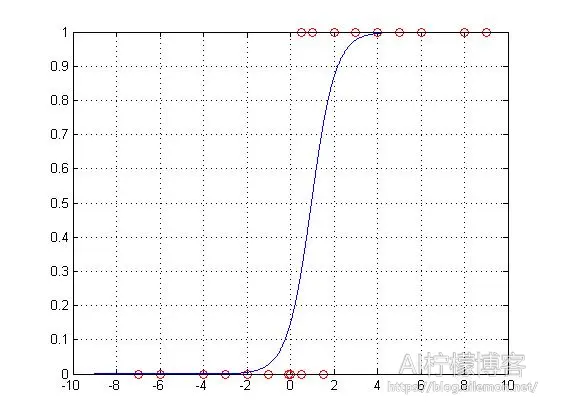
梯度下降自实现：

theta =

-1.7417
1.8136

cost =

0.2007

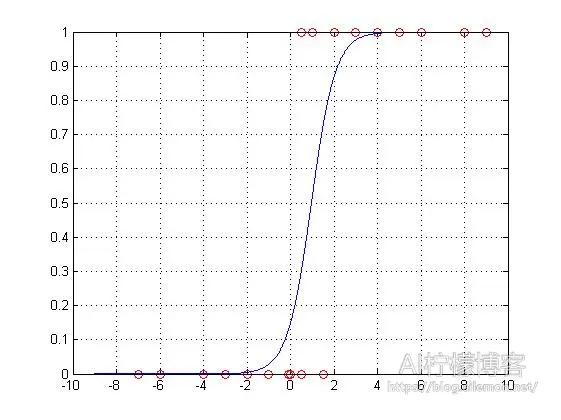
我们可以看到，内置函数和自实现的梯度下降计算得到的结果几乎一样，而且得到的图像也是没有区别的。之后，我们便可以使用训练得到的机器学习模型来预测我们想要预测的事情了。

不过，我前面说过，对数几率回归是感知机和神经网络模型的组成基础，所以我们可以以感知机或神经网络的角度来看待它。将一个对数几率回归看成一个神经元，其参数的训练看成神经元的参数训练，只不过它不含隐藏层而已。本例中的模型可以看成：

而多元变量的对数几率回归，请看我的下一篇文章： 对数几率回归-2

参考资料：
《机器学习·周志华》（清华大学出版社）P57 – P60

MATLAB代码：

CostFunction.m

function [J, grad] = CostFunction(theta, X, y)
%计算对数几率回归的代价函数和梯度
m = length(y); % 训练样例数
J = 0;
grad = zeros(size(theta));
J = sum(-y .* log(sigmoid(X * theta)) - (1 - y) .* log(1 - sigmoid(X * theta)) )/m;
grad = (X' * (sigmoid(X * theta) - y))/m;
end

sigmoid.m

function g = sigmoid(z)
%计算sigmoid函数值
g = zeros(size(z));
g=1./(1+exp(-1.*z));
end

1.使用fminunc函数

logistic_fmin.m

%% 数据
X=[0 2 5 -1 -3 4 -0.1 0.5 9 -6 -4 -3 -2 1 8 -7 6 3 1.5 0.5]';
Y=[0 1 1 0 0 1 0 0 1 0 0 0 0 1 1 0 1 1 0 1]';
plot(X,Y,'ro')
grid on
hold on
%% 初始参数配置
%  获取数据样本数量
[m, n] = size(X);
% 在列向量的左边添加一列全为1的列向量
X = [ones(m, 1) X];
% 初始化拟合参数
initial_theta = zeros(n + 1, 1);
% 计算并显示初始的代价和梯度
[cost, grad] = CostFunction(initial_theta, X, Y)
%% 使用fminunc()函数来最小化代价函数
%  为函数fminunc设置选项
options = optimset('GradObj', 'on', 'MaxIter', 400);
%  运行函数fminunc来获得optimal theta
%  这个函数将返回参数 theta 和代价 cost 
[theta, cost] = fminunc(@(t)(CostFunction(t, X, Y)), initial_theta, options)
%% 数据拟合结果展示
x=[ ones(1,1901) ; -9:.01:10]';
y=sigmoid(x * theta);
plot(x(1902:3802),y)

2.梯度下降自实现

logistic_grad.m

%% 数据
X=[0 2 5 -1 -3 4 -0.1 0.5 9 -6 -4 -3 -2 1 8 -7 6 3 1.5 0.5]';
Y=[0 1 1 0 0 1 0 0 1 0 0 0 0 1 1 0 1 1 0 1]';
plot(X,Y,'ro')
grid on
hold on
%% 初始参数配置
%  获取数据样本数量
[m, n] = size(X);
% 在列向量的左边添加一列全为1的列向量
X = [ones(m, 1) X];
% 初始化拟合参数
theta=zeros(n + 1, 1);
iterations = 1000; % 设置迭代次数
alpha = 0.5; % 设置学习率
% 计算并显示初始的代价和梯度
[cost, grad] = CostFunction(theta, X, Y)
%% 自制梯度下降来最小化代价函数

J_history = zeros(iterations, 1);
for iter = 1:iterations % 这里不用while的原因是一旦出现发散的情况，程序将陷入死循环
    [J_history(iter),grad] = CostFunction(theta, X, Y);
    theta = theta - alpha * grad;
end
%% 数据拟合结果展示
x=[ ones(1,1901) ; -9:.01:10]';
y=sigmoid(x * theta);
plot(x(1902:3802),y)
% 显示结果值
theta
J_history(iterations)

写在最后：
鉴于本人水平有限，如果文章中有什么错误之处，欢迎指正，非常感谢。

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2017/02/12/machine-learning-logistic-regression-1/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate