机器学习：统计回归模型

统计回归方法是当今大多数机器学习方法的基础之一，机器学习的很多工程领域应用都是基于此的推广。在统计学中，线性回归（Linear regression）是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。多项式曲线拟合(Fitting)则是将线性回归推广到了高阶函数中。机器学习中的线性回归和多项式拟合是有监督学习方法。文末附Python和MatLab程序代码。

一、线性回归

1. 模型建立

线性回归最典型的一个实例就是预测房价，即房产总价与购买的房屋面积的关系，还可以用来预测买一个移动硬盘的价钱，即移动硬盘的总价和容量大小的关系，这是最简单的一元线性回归。线性回归的通式为：

y = θ^T * x

其中，a是一个二维的列向量 [θ₀ ; θ₁ ]，而二维列向量x是 [ 1 ; x₁ ]。因为是一元线性回归，所以根据线性代数知识，上式实际可以写为：

y = θ₀ + θ₁ * x₁

         我们都知道，房价跟房屋面积肯定是正相关的，但是并不是成正比的，具体的房价受制于多种因素，但最主要的因素是面积，这是毋庸置疑的，移动硬盘也是同样的道理。所以我们可以暂且忽略其他因素，抓住主要矛盾，研究房价与面积的关系，移动硬盘价格和容量的关系。

当然，我们知道，其他的因素是有影响的，如果我们想加入其它因素（比如房子距离市中心的距离，移动硬盘的尺寸）的话，只要再多一维或者几维的数据，然后进行同样的训练即可，其他的原理是一样的。我们就仅以预测房价为例。

我们有某市这样的一组数据用来训练：

面积 (m2)	40.10	63.50	65.13	80.15	85.62	91.22	95.56	98.36	100.56	120.32
总价 (万元)	39.86	65.99	64.98	80.10	85.65	92.11	95.10	99.12	101.23	119.85

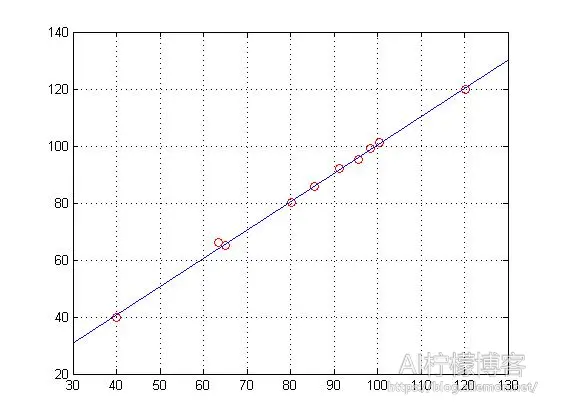
将面积值存到变量X中，总价则存到变量Y中，然后做线性回归。在MATLAB中，我们可以直接使用polyfit()和regress()函数来实现。得到的图像如下图，我们可以看到，数据样本点均匀分布在直线的两侧。

既然是线性回归，得到的直线方程必须能够最优地拟合数据，也就是说，我们必须让数据到拟合直线的方差最小。为了表示这个方差，我们可以定义一个代价函数(Cost Function)来表示这个量：

其中，m为数据量。

我们的目标是要寻找一个合适的参数θ，使得代价函数最小。对于这个参数的估计，可以使用矩估计法、最大似然估计法，或者比较常用的最小二乘法。在这里，我们使用最小二乘法，不过，我们将使用梯度下降(Gradient Descent)来实现。

2. 梯度下降

梯度下降是迭代法的一种，可以用于求解最小二乘问题（线性和非线性都可以）。梯度下降作为一种非常的受欢迎的优化算法，使用极其广泛，神经网络中的参数也是常常使用梯度下降来求解的。梯度下降的几何过程如果所示：

从其中一点出发，沿着梯度的相反方向走一小步，然后在所到的位置处，再沿着梯度的相反方向走一小步，如此下去，直到走到“山谷”为止，即收敛。不过，使用梯度下降的时候，有时候并不能收敛到全局最小值，而是陷入到了局部的极小值，如上图所示。由图可以看出，从不同的两点，经过梯度下降，收敛到了不同的极小值点。为了解决这一个问题，我们可以随机地从不同的几个点分别开始梯度下降，可能会收敛到不同的极小值点，这时，我们选取其中值最小的一点作为结果即可。虽然这样也并不能保证一定收敛到全局最优点，但是概率已经是很大的了。

不过，在这个问题中，我们的代价函数是凸函数，他的极小值就是全局最小值，所以，我们无需担心陷入局部最优。更确切地说，一切凸函数都只有一个极小(大)值，这个极小(大)值点就是最小(大)值点。这里的凸函数是广义上的凸函数。当然，我们也可以多选几个初始点来做梯度下降，因为一些偶然因素，最终的代价值还是略微有所不同的，那么就选最小的那种。

当然，梯度下降也有他的缺点，比如靠近极小值时速度减慢，直线搜索可能会产生一些问题，可能会“之字型”地下降等。但是瑕不掩瑜，这并不能成为阻碍梯度下降法受欢迎的绊脚石，因为梯度下降法的优势是很明显的。

我们通过梯度下降方法来持续更新参数θ，直到他收敛，那么，我们更新参数的公式为：

(对于所有的j，需同时更新参数θ_j)

其中，参数α为初始学习速率，代表着梯度下降的速率，需要选择一个合适的参数。

在学习速率为固定值的时候，这个参数不能太小，否则学习的步数太多，程序的速度很慢，你可能需要很长一段时间才能收敛；但是也不能选的太大，否则，你可能会发现，或许一开始J很快就接近收敛了，但是步长太大，之后并没有收敛，而是出了点状况。你会发现，代价函数的值不但迟迟不收敛，反而可能会越来越发散，以至于结果变得糟糕起来，甚至会导致直接跨过谷底到达另一端，这就是所谓的“步子太大，迈过山谷”。至于这个参数如何选择，需要有一定的经验，不过可以提前多选几个值做一下试验，比如用0.001，发现太慢，用0.1，发现过一段时间会发散，0.01既不太慢也不会发散，那就选择这个参数。

或者我们可以根据梯度下降每一步的实际情况动态调整学习速率，使用可变的学习速率，这就是上式的由来。我们设定一个初始的学习速率，这个学习速率也不能太大，否则一开始就会发散，当然也不能太小，否则速度太慢。在优化的过程中，学习速率应该逐步减小，越接近“山谷”的时候，迈的“步伐”应该越小。我们每走一步，数据分布与直线的误差越小，而这时梯度也会减小，那么步伐也就应当相应的减小，这就是初始学习速率乘上代价函数负梯度的原因。本实例中，经过我的试验，学习速率选择为0.0001比较合适。

值得说明的是，在进行梯度下降的时候，我们应当尽量使用限定迭代次数的循环，而不是用判断是否收敛的循环。原因很简单，一旦出现你的结果是发散的，限定迭代次数的循环可以使你的程序很快停止下来，而因为你的结果永远不会收敛，所以，如果你用while进行判断是否收敛的话，你将很有可能陷入死循环，因为你的结果永远不可能收敛。这里我把迭代步数设为100步。

经过训练，我们得到训练后的结果：

theta =

0.0118

1.0033

J =

0.3812

即  回归直线方程为 y = 0.0118 + 1.0033 * x

代价为 0.3812

训练后，得到的回归直线的图像为：

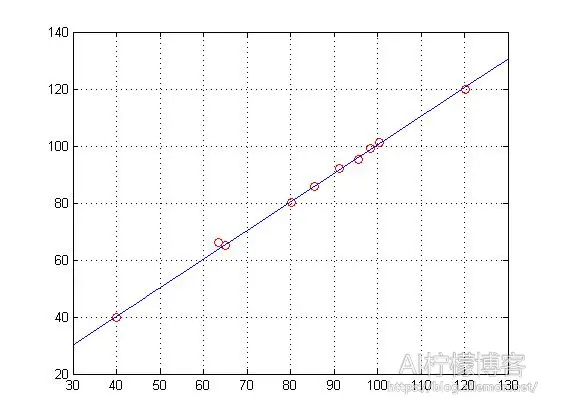
由图可见，这个结果与MATLAB的回归拟合函数的结果是基本一样的。不过细心的人会发现一个问题，这两种方式的一次项参数θ(2)的值比较接近，但是常数项参数θ(1)的值差别较大，MATLAB内置拟合函数结果接近1，而梯度下降的结果接近0.01，不过函数图像差不多。这是因为对参数θ的估计方式不同导致的，而由图像明显可以看出，这一差别并没有产生什么大的影响，所以，我们暂且可以忽略它。

二、二次回归与多项式拟合

顾名思义，二次回归就是使用最高次数为二次的多项式来做统计回归，这属于非线性回归模型，是线性回归模型的拓展。而训练这样一类模型，就是用多项式做曲线拟合，同样使得代价函数最小即可。

我们有一组数据，但是我们看不出来是使用线性回归好，还是二次回归好，或者更高次的多项式拟合好，怎么办？这里有一种方法，从一次回归一直到十次全部尝试一遍，然后看哪一种拟合使得代价函数值最小，选取值最小的那一种拟合方式进行拟合即可。

不过，随着神经网络的火热发展，一般多项式的拟合都可以使用神经网络来代替。神经网络有着强大的函数表示能力，它既可以表示线性的函数，又可以表示非线性的函数，而且隐藏层越多，表示能力越强。

参考资料：

1.【线性回归 – 维基百科】

2.【梯度下降法 – 维基百科】

程序代码：

Python代码 (Python3)

import numpy as np
import matplotlib.pyplot as plt  


# 数据  
X=[40.10, 63.50, 65.13, 80.15, 85.62, 91.22, 95.56, 98.36, 100.56, 120.32]
Y=[39.86, 65.99, 64.98, 80.10, 85.65, 92.11, 95.10, 99.12, 101.23, 119.85]
X=np.matrix(X).T
Y=np.matrix(Y).T
# 初始化和准备工作
theta = np.zeros((2, 1), dtype = np.float) # 初始化拟合参数

# 一些梯度下降参数设置
iterations = 100 # 设置迭代次数
alpha = 0.0001 # 设置学习率
(m,n) = X.shape# 计算训练数据的数量 

XX=np.hstack((np.ones((m, 1), dtype = np.float), X))# 在原来X的左边添加一行全为1的列向量

J = sum(np.power((XX * theta - Y),2)) / (2*m)#    计算初始的代价
# 开始梯度下降，结束后得到训练完毕的参数theta
J_history = []
for iter in range(0,iterations): # 这里不用while的原因是一旦出现发散的情况，程序将陷入死循环
    
    theta = theta - alpha * 1/m * (XX.T * (XX * theta - Y))
    # Save the cost J in every iteration
    print(iter,'\n',theta,'\n')
    cost = np.sum(np.power(XX * theta - Y,2)) / (2*m) 
    J_history.append(cost)#     XX(10,2)  theta(2,1)

# 显示训练结果和原始数据分布
J = np.sum(np.power((XX * theta - Y),2)) / (2*m)#     计算代价
print('Cost:',J)

x = np.arange(30, 1000) * 0.1
x=np.matrix(x).T
x_m = x.shape
xx=np.hstack((np.ones((x_m[0], 1), dtype = np.float), x))
y=xx*theta
 
plt.plot(x, y)   
plt.show() 

MATLAB (可运行于Octave)

1. polyfit()函数实现

X=[40.10 63.50 65.13 80.15 85.62 91.22 95.56 98.36 100.56 120.32]';
Y=[39.86 65.99 64.98 80.10 85.65 92.11 95.10 99.12 101.23 119.85]';
plot(X,Y,'ro')
hold on
p=polyfit(X,Y,1)
x=[30:.1:130];
y=p(1)*x + p(2);
plot(x,y)
grid on

2.regress()函数实现

X=[40.10 63.50 65.13 80.15 85.62 91.22 95.56 98.36 100.56 120.32]';
Y=[39.86 65.99 64.98 80.10 85.65 92.11 95.10 99.12 101.23 119.85]';
X=[ones(10,1), X];
[theta,bint,r,rint,stats]= regress(Y,X)
plot(X(11:20),Y,'ro')
hold on
x=[30:.1:130];
y=theta(1)+theta(2)*x;
plot(x,y)
grid on

3.梯度下降实现

%% 数据  
X=[40.10 63.50 65.13 80.15 85.62 91.22 95.56 98.36 100.56 120.32]';
Y=[39.86 65.99 64.98 80.10 85.65 92.11 95.10 99.12 101.23 119.85]';

%% 初始化和准备工作
theta = zeros(2, 1); % 初始化拟合参数
%theta = 2*ones(2, 1);
% 一些梯度下降参数设置
iterations = 100; % 设置迭代次数
alpha = 0.0001; % 设置学习率
[m,n] = size(X);  % 计算训练数据的数量 
XX = [ones(m, 1), X]; % 在原来X的左边添加一行全为1的列向量
J = sum((XX * theta - Y).^2) / (2*m)     % 计算初始的代价

%% 开始梯度下降，结束后得到训练完毕的参数theta
J_history = zeros(iterations, 1);
for iter = 1:iterations % 这里不用while的原因是一旦出现发散的情况，程序将陷入死循环
  theta = theta - alpha * 1/m * (XX' * (XX * theta - Y))
    % Save the cost J in every iteration    
    J_history(iter) = sum((XX * theta - Y).^2) / (2*m);     % XX(10,2)  theta(2,1)
end

%% 显示训练结果和原始数据分布
J = sum((XX * theta - Y).^2) / (2*m)     % 计算代价

plot(X,Y,'ro')
hold on
x=[30:.1:130]';
[x_m,x_n]=size(x);
xx=[ones(x_m,1), x];    %添加一列全为1的向量
y=xx*theta;
plot(x,y)
grid on

写在最后：

鉴于本人水平有限，如果文章中有什么错误之处，欢迎指正，非常感谢。

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2017/02/10/machine-learningregression-statistic-model/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate