机器学习引言

作为一个学习机器学习有一段时间的人，很理解那些还一点都不知道机器学习为何物的人的着急，因为我当时就是那样，我想以自己的语言来尽量通俗易懂地把它讲出来，以便帮助他们入门。

         机器学习是人工智能的一个分支，涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科，已广泛应用于数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语音和手写识别、战略游戏和机器人等领域。

按照机器学习任务类型的不同，可分为有监督式学习和无监督式学习，以及半监督式学习和增强学习。
—-WikiPedia.org

俗话说：“朝霞不出门，晚霞行千里”。这句话说的是如果有朝霞，那么就很有可能下雨，就不要出门了，而如果有晚霞，那么就可以出远门了，不会下雨。为什么古人会将朝霞晚霞与是否下雨联系起来呢？

这是古人根据自然现象长期观察的结果，尽管由于科学技术条件限制，古人并不会知道这两者之间有什么因果关系。古人通过长期生活发现，出现朝霞往往会下雨，而出现晚霞则往往是晴天，那么我们就可以得出这个结论。

机器学习也是这样的一个过程。假设观测现象朝霞表示为0，晚霞表示为1，符号为X，而对应结果下雨表示为1，不下雨表示为0，符号为Y，那么我们可以收集到这样的数据：

X	0	1	0	0	1	0	1	1
Y	1	0	0	1	0	1	0	1

如果我们使用统计回归模型做线性回归(Linear Regression)，将其画到坐标纸上，那么可以得到这样的直线：

y = -0.5 * x + 0.75

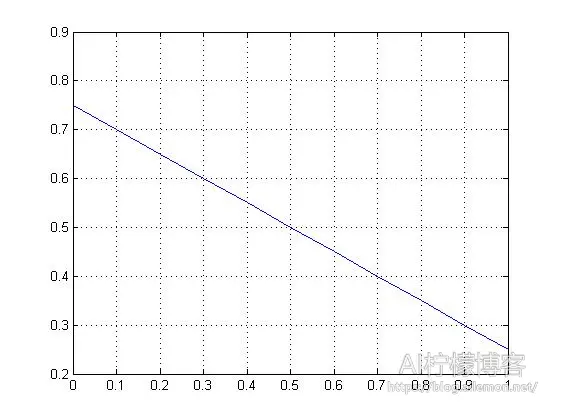
Figure 1

从图中我们可以认为当出现0即朝霞的时候，降水概率很大，而当出现1即晚霞的时候，降水概率很小。

这是有监督学习的一个典型应用，我们收集已知的观测数据X和其对应的标签Y，然后作为训练集(Training Set)，输入到模型中，然后我们使其方差（代价函数，Cost Function）最小，即最大程度拟合我们的训练数据，我们就得到了一个机器学习模型，然后我们可以使用测试集(Test Set)去验证我们的模型，测试一下模型的正确率。我们还可以使用这种模型去做房价的预测之类的事情。

当然，我们也可以使用对数几率回归模型(Logistic Regression Model)来做二分类。虽然对数几率回归听起来是回归模型，但是它其实是一种分类模型的算法。他所使用的拟合函数是一种S型的函数(Sigmoid Function)，其实这个天气问题在这种分类模型下表现会更好一些。Sigmoid函数的通用表达式如下：

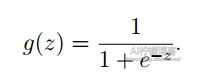
它的图形如果你有兴趣可以自己试一试画出来，它的形状就像字母S一样。

Logistic Regression的函数定义如下：

h_θ(x) = g(θ^T x)

因此，我们使用这个模型进行拟合，同样使其方差（代价函数，Cost Function）最小，我们大致上可以得到这样的图形：

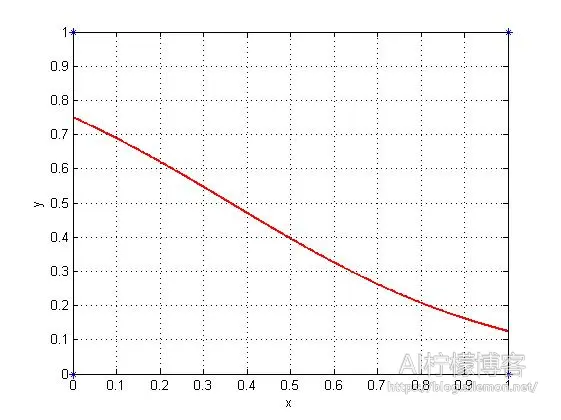
Figure 2

我们可以设置一个阈值为0.5，当结果>=0.5的时候，我们就将其结果划分为1，否则划分为0，那么我们就可以得到当x=0时y=1和当x=1时y=0了，即我们所要得到的结论。

这也是有监督学习的一个应用。当然，Logistic Regression的能力远超于此，它是神经网络模型的基础，而现在非常火热的深度学习则是神经网络模型发展演变而来的，限于篇幅以及我目前的水平，我之后再做详细介绍。

在这个关于天气问题中，各个值都是离散的，似乎0和1中间的那些连续的值并没有什么意义，不过我们也可以赋予他们一些意义，比如朝霞出现的程度或者晚霞出现的程度等，不过这不好判定。

俗话说：“物以类聚，人以群分”，聚类也是机器学习的一种算法，它属于无监督学习。举个例子，比如我们在网上购物，而每一个用户都有他们自己的偏好，比如A喜欢买一些电脑配件，B喜欢购买一些科技类书籍，C喜欢购买一些文学书籍，D喜欢买一些零食。这是典型的不同的4类人群。当然，我们可以认为B和C的偏好有所接近，因为他们都喜欢书，这也是没错的。如果我们定义一个向量X，X(1)代表电脑配件，X(2)代表书籍，X(3)代表偏好科技类的内容，X(4)代表偏好文学类内容，X(5)代表喜欢吃。那么我们可以以此来对每一个人的浏览习惯做一个包含以上内容的记录，每一个人都有他自己的偏好特征向量。假设我们收集了1000个人的数据，那么我们可以使用余弦定理进行聚类。

有人说：“余弦定理也能做机器学习？”确实是这样，我们收集到了每个人的特征向量，它是高维空间的向量，然后我们根据向量夹角的余弦定理，设置一个阈值，比如0.9吧。当余弦值>=0.9的时候，我们就认为某两个向量相似，这样我们就实现了聚类，最后得到的类别数目取决于具体数据的情况。同样的，我们也经常使用欧氏距离（欧几里得距离）来实现聚类。

聚类不是目的，只是一种实现目的的手段，聚类之后，我们能做一些什么事情呢？比如推荐系统。推荐系统有多种运作方式，比如给物品根据特征打上标签之后，我们进行聚类后可以实现在用户浏览某一物品时推荐一些相似的物品；也可以对用户的偏好特征进行聚类，然后某一用户购买了某些商品之后，给其他同类的用户也推荐这些商品。通过推荐系统，来实现电商和卖家利润的最大化。

推荐书籍：

【机器学习 周志华】清华大学出版社

【数学之美 吴军】人民邮电出版社

这两本书是入门机器学习重要的书籍，尤其是周志华教授的那本“西瓜书”，讲的很基础，跟市面上一些其他的大段的公式和推理证明的书不同，这本书能够让你很轻松入门机器学习，本科生就可以看懂。至于吴军老师的那本《数学之美》，以自己的一些真实故事来讲解数学的应用，其中包含了不少机器学习、自然语言处理等方面的内容。我想高中生水平就可以看懂，更基础，而且通俗易懂，可以极大地提高你对数学的兴趣。当然，数学是很重要的。

参考资料：

【机器学习 – 维基百科】

【余弦相似性 – 维基百科】

【聚类分析 – 维基百科】

【推荐系统 – 维基百科】

附录：

MATLAB代码

1.

X=[0 1 0 0 1 0 1 1];
Y=[1 0 0 1 0 1 0 1];
plot(X,Y,'o');
p=polyfit(X,Y,1);
x=[0:.1:1];
y=p(1)*x+p(2);
plot(x,y)
grid on;

2.

x=[0 1 0 0 1 0 1 1]';
y=[1 0 0 1 0 1 0 1]';
st_ = [0.5];
ft_ = fittype('1/(1+7*exp(-r*(x-1))) ' ,...
     'dependent',{'y'},'independent',{'x'},...
     'coefficients',{'r'});
[cf_ ,good]= fit(x,y,ft_ ,'Startpoint',st_)
h_ = plot(cf_,'fit',0.99); %置信系数0.99
legend off;  % turn off legend from plot method call
set(h_(1),'Color',[1 0 0],...
     'LineStyle','-', 'LineWidth',2,...
     'Marker','none', 'MarkerSize',6);
 hold on,plot(x,y,'*') 
 grid on

写在最后：

鉴于本人水平有限，如果文章中有什么错误之处，欢迎指正，非常感谢。

版权声明 本博客的文章除特别说明外均为原创，本人版权所有。欢迎转载，转载请注明作者及来源链接，谢谢。 本文地址: https://blog.ailemon.net/2017/02/02/introduction-to-machine-learning/ All articles are under Attribution-NonCommercial-ShareAlike 4.0

Donate

WeChat DonateAlipay Donate